Appendix 1. N Queens パズル

1. 初めに

今までの説明で通常のプログラムは書けるようになったので、今回は復習をかねて、 N Queen パズルを取り上げます。このパズルは N x N のチェス盤の上に N 個の Queen を互いの利き筋が重ならない（つまり、一手ではお互いに取られない）ように置くパズルです。Queen はチェスの駒で、縦横、斜めに駒にぶつかるか、盤の端に来るまで好きなだけ動けます。（日本将棋の飛車と角を合わせた動きをします。）

８ x 8 のチェス盤の場合、解は 92 個あります。チェス盤の対称操作を考慮すると独立の解は 12 個になります。ここでは、対称操作を考慮した解を求めてみます。このパズルを解くプログラムには再帰関数がふんだんに出てくるので Scheme 向きの問題といえます。 Scheme である程度大きいプログラムを書くとどんな感じになるか見てください。

2. パズルの解き方

2.1. 縦横の利きの避け方

Queen は縦横に利いているので、それぞれの行と列には Queen は１つずつしか入れません。従って、0 から (n-1) の整数の順列を作り、数が行、数の位置が列を表すようにすれば、縦横の利きはぶつかりません。(図１）後は斜めの利きがぶつからないようにしながら Queen を置いていけば解けます。

'(3 1 6 2 5 7 4 0)

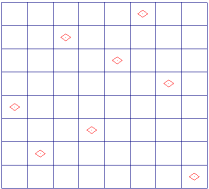
図１：0 から (n-1) の整数の順列を作り、数が行、数の位置が列を表すようにすれば、縦横の利きは避けることができる。

2.2. 斜めの利き避け方

Queen は盤の右から左に向かって置いていきます。

新しく置かれた Queen の行の位置を p とすると、隣の列での斜めの利きは (p+1), (p-1) となり、列の移動に伴って１つ増えるか、１つ減るかします。従って、新しく置かれた Queen q がすでに盤上にある Queen qs とぶつかるかどうかは次の関数で調べることができます。（2.1. の方針に従って縦横はぶつからないことが保証されているとします。）

[code 1]

;; check if queens conflict each other
(define (conflict? q qs)
  (let loop((up (inc q)) (down (dec q)) (ls0 qs))
    (if (null? ls0)
        #f
      (let ((c (car ls0)))
        (or
         (= c up)
         (= c down)
         (loop (inc up) (dec down) (cdr ls0)))))))

関数 conflict? は Queen の利きが衝突すれば #t をしなければ #f を返します。ここで (inc x), (dec x) は引数 x に１を加える、1 を引く関数です。

2.3. Queen を盤に置いていく

Queen を盤に置いていくには [code 2] に示す q-add を使います。 q-add は queen の内部関数です。

[code 2]

    (letrec ((q-sethash (lambda (qs)                 ;; registrate on the hash table
                          (let ((qi (q2int n qs)))
                            (when (eq? (hashtable-ref qsol qi 'not-yet) 'not-yet)
                                 (for-each
                                  (lambda (op)
                                    (hashtable-set! qsol (q2int n (op qs)) #f))
                                  (list t90 t180 t270 reverse usd d1 d2))
                                 (hashtable-set! qsol qi #t)))))
                          
              
             (q-add (lambda (qs i pool)             ;; adding new queen
                      (if (= i n)
                          (q-sethash qs)
                        (for-each (lambda (x)
                                    (or (conflict? x qs)
                                        (q-add (cons x qs) (inc i) (remove x pool))))
                                  pool)))))

q-add はすでに盤上にある Queen のリスト qs と置かれている Queen の数 i とまだ使われていない行のリスト pool の３つの引数をとります。置かれている Queen の数が n に等しいときは、q-sethash 補助関数を使って解をハッシュ表に登録します。そうでなければ、pool に残っている行について、すでに置かれている Queen と衝突するか調べ、衝突しなければ、それを盤上に加え、pool からそれを取り除いて、 q-add を繰り返します。 (remove x ls) は ls から x を取り除いたリストを返す関数です。付録の nqueen.scm にその定義があります。

2.4. 解をハッシュ表に登録する

[code 2] の補助関数 q-sethash を使って解をハッシュ表に登録します。

q-sethash では、まず、解を q2int で整数に変えてハッシュ表のキーにします。次に、解がすでにハッシュ表に登録されているか調べます。もし、登録されていなければ、対称操作で生ずる盤面を値 #f で登録し、その後、もとの盤面を値 #t で登録します。こうすると、対称操作で互いの変換できない独立した解のみが値 #t でハッシュ表に登録されます。

N Queens を解く関数 (queen n) は [code 3] のようになります。 24 行目の (q-add () 0 (range n))) でを探し始め、25--27 行目で独立解を選び出し、 28 行目でプロットします。値が何も返らないと落ち着かないので、解の数を返すようにします。

[code 3]

;;; the main function
(define (queen n)
  (let ((qsol (make-eqv-hashtable))
        (qlist '()))
    (letrec ((q-sethash (lambda (qs)                 ;; registrate on the hash table
                          (let ((qi (q2int n qs)))
                            (when (eq? (hashtable-ref qsol qi 'not-yet) 'not-yet)
                                 (for-each
                                  (lambda (op)
                                    (hashtable-set! qsol (q2int n (op qs)) #f))
                                  (list t90 t180 t270 reverse usd d1 d2))
                                 (hashtable-set! qsol qi #t)))))
                          
              
             (q-add (lambda (qs i pool)             ;; adding new queen
                      (if (= i n)
                          (q-sethash qs)
                        (for-each (lambda (x)
                                    (or (conflict? x qs)
                                        (q-add (cons x qs) (inc i) (remove x pool))))
                                  pool)))))
                      
            (q-add '() 0 (range n)))
    (let-values (((key value) (hashtable-entries qsol)))  ; pick up distinct solutions
                (vector-for-each
                 (lambda (k v)
                   (when v (set! qlist (cons (int2q n k) qlist))))
                 key value))
    (qplot n qlist)   ;; plotting the distinct solutions
    (length qlist)))

2.5. 対称操作

対称操作には、動かさないという操作のほかに、90, 180, 270 度回転、上下、左右、対角線（２つ）反転の７つがあります。回転は、N Queens パズルの性質から、0 -- (n-1) の数の列の位置を返すと 90 度回転になります。対称操作関数を [code 4] に挙げます。

[code 4]

;;; symmetry operations
;; turn 90 degree
(define (t90 qs)
  (let ((n (length qs)))
    (let loop ((ls1 '()) (i 0))
      (if (= i n)
          ls1
        (loop (cons (position i qs) ls1) (inc i))))))

;; turn 180 degree
(define (t180 qs)
  (usd (reverse qs)))

;; turn 270 degree
(define (t270 qs)
  (t90 (t180 qs)))

;; up side down
(define (usd qs)
  (let ((n (dec (length qs))))
    (map (lambda (x) (- n x)) qs)))

;; reflection on diagonal 1
(define (d1 qs)
  (reverse (t90 qs)))

;; reflection on diagonal 2
(define (d2 qs)
  (usd (t90 qs)))

2.6. 結果の表示

結果の表示には gnuplot を使います。

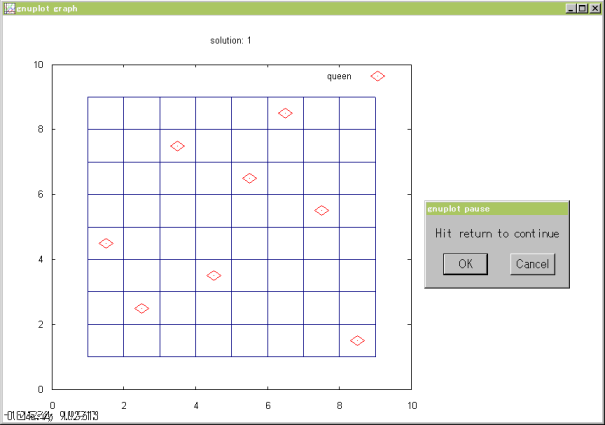
MzScheme にはグラフィック用ライブラリがありますが、gnuplot に書かせたほうが簡単です。表示の部分のコードを [code 5] に示します。i 番目の解に対して qi.dat というデータファイルをつくり、それを queen.plt というコマンドファイルでプロットします。 gnuplot のコンソールに
load 'queen.plot'
と与えると、図に示すプロットが表示され、ダイアログで 'OK' をクリックすると次の解が表示されます。

図２： N Queen パズルの解の表示 [code 5]

;;; plotting using gnuplot
;; drawing grid
(define (draw-grid n)
  (let ((p (number->string (inc n))))
    (let loop((i 0))
      (when (<= i n)
          (let ((s (number->string (inc i))))
            (print-lines
             (string-append "set arrow from " s ", 1 to " s ", " p " nohead lt 5")
             (string-append "set arrow from 1, " s " to " p ", " s " nohead lt 5"))
            (loop (inc i)))))))
    

;; plotting data file of the solution
(define (plot-queen len)
  (let loop((i 0))
    (when (< i len)
         (print-lines
          (string-append "set title \"solution: " (number->string (inc i)) "\"")
          (string-append "plot \"q" (number->string i) ".dat\" title \"queen\" with point pointsize 3")
          "pause -1 \"Hit return to continue\"")
         (loop (inc i)))))

;; writing data files
(define (q-write-dat qls)
  (let loop((i 0) (ls qls))
    (when (pair? ls)
         (with-output-to-file (string-append "q" (number->string i) ".dat")
            (lambda ()
              (let rec((j 0) (ls1 (car ls)))
                (when (pair? ls1)
                     (print-lines (string-append (number->string (+ j 1.5)) " " (number->string (+ (car ls1) 1.5))))
                     (rec (inc j) (cdr ls1))))))
         (loop (inc i) (cdr ls)))))
                   
;; making a command file for gnuplot                
(define (qplot n qls)
  (q-write-dat qls)
  (with-output-to-file "queen.plt"
    (lambda ()
      (let ((s (number->string (+ n 2))))
        (print-lines
         "reset"
         "set size square"
         (string-append "set xrange [0:" s "]")
         (string-append "set yrange [0:" s "]"))
        (draw-grid n)
        (plot-queen (length qls))))))

3. 付録の使い方

付録には nqueen.scm が入っているので、次のようにして遊んでください。

付録を解凍して生じた nqueen.scm を MzScheme で load する。

(queen n) を実行する。

C:\doc\scheme>mzscheme
Welcome to MzScheme v4.0.2 [3m], Copyright (c) 2004-2008 PLT Scheme Inc.
> (load/cd "nqueen.scm")
> (queen 8)
12

gnuplot で、'load queen.plt' として、解を表示させる。

練習問題 1

[code 3] の関数 queen を改造して、 N Queens パズルの解のうち、対称性を持つ解を求める関数 queen_sym を書いてください。
また、N Queens の性質から、どういう対象性が許されるか考えてください。

4. 終わりに

今回は今までの復習として少し大きめのプログラムを書いてみました。大き目といっても、200 行弱で、そのうち、汎用ユーティリティが 40 行、出力が 50 行占めています。単にリストを返すだけなら 150 行弱で書けることになります。

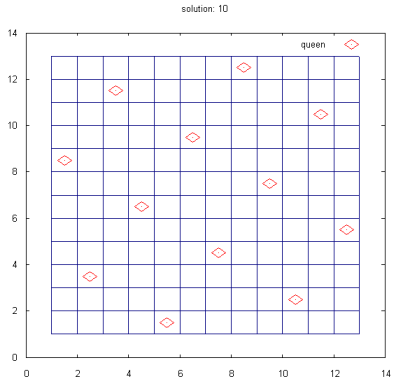
ソースコードを見ていただくとわかるように、queen を除く全ての関数が 20 行以下で書かれています。 Scheme ではこのように小さい関数を積み上げてプログラムを作っていきます。

練習問題の解答

練習問題 1

q-sethsh を少し変えて、対称操作によって、自分自身に重なるものだけをハッシュ表に登録します。
反転対称性をもつ解は Queen の利き筋から存在しません。90 度回転の対称性を持つ解は珍しく、 13x13 以下では 4x4, 5x5, 12x12, 13x13 の場合にしかありません。(図３）ほとんどは 180 度回転の対象性を持ちます。

図３：90 度回転対称性を持つ解

;; make my own memv as memv in MzScheme require a 'proper list'
(define (my-memv obj ls)
  (cond
   ((null? ls) #f)
   ((= obj (car ls)) #t)
   (else (my-memv obj (cdr ls)))))

;;; the main function to find symmetrical solutions
(define (queen_sym n)
  (let ((qsol (make-eqv-hashtable))
        (qlist '()))
    (letrec ((q-sethash (lambda (qs)                 ;; registrate on the hash table
                          (let ((qi (q2int n qs)))
                            (when (not (hashtable-contains? qsol qi))
                              (let ((ls_sym (map (lambda (op) (q2int n (op qs))) `(,t90 ,t180 ,t270 ,reverse ,usd ,d1 ,d2))))
                                (when (my-memv qi ls_sym)
                                      (for-each
                                       (lambda (v)
                                         (hashtable-set! qsol v #f))
                                       ls_sym)
                                  (hashtable-set! qsol qi #t)))))))

                          
             (q-add (lambda (qs i pool)             ;; adding new queen
                      (if (= i n)
                          (q-sethash qs)
                        (for-each (lambda (x)
                                    (or (conflict? x qs)
                                        (q-add (cons x qs) (inc i) (remove x pool))))
                                  pool)))))
                      
            (q-add '() 0 (range n)))
    (let-values (((key value) (hashtable-entries qsol)))  ; pick up distinct solutions
                (vector-for-each
                 (lambda (k v)
                   (when v (set! qlist (cons (int2q n k) qlist))))
                 key value))
    (qplot n qlist)   ;; plotting the distinct solutions
    (length qlist)))