17. 遅延評価

1. 初めに

遅延評価 (lazy evaluation) とは、値が必要になるまで計算しないという計算方法です。この方法の利点はデータに繰り返し構造を自然に組み込むことができ、無限を簡潔に表現できることです。これによって、プログラムのモジュール化が促進され、プログラムが美しくなります。遅延評価の利点についてはなぜ関数プログラムは重要かを見てください。

全体的に遅延評価を取り入れた言語としては Haskell が有名ですが、 Scheme も部分的に遅延評価を取り入れています。

2. 遅延評価にかかわる関数

R⁵RS では遅延評価にかかわる関数として次のものが用意されています。評価法が指示されているが実際の計算が行われていない中間状態をプロミスといい、プロミスを強制 (force)することで値が計算されます。

(delay proc): proc をプロミスにします。
(promise? obj): obj がプロミスなら #t を返します。
(force promise): promise から値を計算します。

3. 遅延評価の簡単な例

遅延評価の簡単な例を [sample 1] に挙げます。このサンプルでは、(+ 1 2) を delay をつかって一度プロミスにしてそれに force を作用させて値を取り出しています。
[sample 1]

> (define laz (delay (+ 1 2)))
> laz
#<promise:laz>
> (promise? laz)
#t
> (force laz)
3
> (* 10 (force laz))
30

ここで注意したいのはプロミスは force によって消費されず、プロミスのままだということです。つまり、force はプロミスから値を計算しますが、プロミスに副作用は及ぼしません。従ってプロミスは何度でも使いまわすことができます。

4. 遅延評価を使った無限リストの表現

それでは早速遅延評価を利用して無限リストを表現しましょう。まず、無限リストを表現するための基本関数を定義し、それからそれらを使って数列を表現し、また、数値計算への応用を示します。

無限リストは、

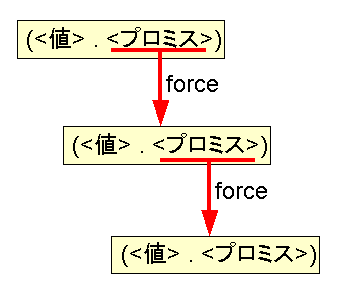
(<val> . <promise>)    (1)

の様に、car 部が確定した値で、cdr 部がプロミスからなっているコンスセルで表します。 cdr 部のプロミスを force するとまた、(1) のようなコンスセルが生成するような入れ子構造を作ることによって無限リストを表します（図１）。コンスセルの入れ子による表現は、通常のリストと同じですが、 cdr 部をプロミスにすることによって通常のリストとは異なり、無限リストが表現できるようになります。

図１：値とプロミスからなるコンスセルによる無限リストの実装。

4.1. 無限リストを表現するための基本関数とマクロ

[code 1] に無限リストを扱うための関数とマクロを示します。この中で最も重要なのが lazy-map でこれを使って無限リストの演算をします。また、 lazy-cons は評価を遅らせるという特殊形式 delay を含むので、マクロ定義にする必要があります。関数で定義すると、評価を遅らせたい式が、引数でわたったとたんに評価されてしまいます。

[code 1]

01:     ;;;;; basic functions and a macro
02:     
03:     ;;; car for lazy evaluation
04:     (define lazy-car car)
05:     
06:     ;;; cdr for lazy evaluation
07:     (define (lazy-cdr ls)
08:       (force (cdr ls)))
09:     
10:     ;;; lazy cons
11:     (define-syntax lazy-cons
12:        (syntax-rules ()
13:           ((_ a b) (cons a (delay b)))))
14:     
15:     ;;; lazy map
16:     (define (lazy-map fn . lss)
17:       (if (memq '() lss)
18:           '()
19:         (lazy-cons (apply fn (map lazy-car lss))
20:                    (apply lazy-map fn (map lazy-cdr lss)))))
21:     
22:     ;;; lazy filter
23:     (define (lazy-filter pred ls)
24:       (if (null? ls)
25:           '()
26:         (let ((obj (lazy-car ls)))
27:           (if (pred obj)
28:               (lazy-cons obj  (lazy-filter pred (lazy-cdr ls)))
29:             (lazy-filter pred (lazy-cdr ls))))))
30:     
31:     ;;; returns n-th item of the lazy list
32:     (define (lazy-ref ls n)
33:       (if (= n 0)
34:           (lazy-car ls)
35:         (lazy-ref (lazy-cdr ls) (- n 1))))
36:     
37:     ;;; returns first n items of the ls
38:     (define (head ls n)
39:       (if (= n 0)
40:           '()
41:          (cons (lazy-car ls) (head (lazy-cdr ls) (- n 1)))))

(lazy-car ls): car 部は確定した値なので、(car ls) と同じです。
(lazy-cdr ls): (cdr ls) の cdr 部（プロミス）を force を使って値を取り出します。
(lazy-cons a b): (cons a (delay b)) に展開されるマクロです。関数定義だと、b が先に評価されてしまうので delay の意味がなくなります。
(lazy-map fn . lss): 遅延評価用の map です。ここで定義する遅延評価用関数の中で最も重要なものです。確定した値と、プロミスからなるコンスセルを返すことに注目してください。
(lazy-filter pred ls): 遅延評価用の filter です。無限リスト ls のうち pred が #t になるものからなるリストを返します。
(lazy-ref ls n): 遅延評価リスト ls の n 番目の要素を返します。
(head ls n): 遅延評価リスト ls の最初から n 番目までの要素の部分リストを返します。

4.2. 無限数列

lazy-cons, lazy-map を使うと無限数列が簡潔に表現できます。ここでは、

等差数列、等比数列などのように次の項が前の項の関数として現される数列
Fibonacci 数列

を例にとって説明します。

4.2.1. 次の項が前の項の関数で表される数列

次の項が前の項の関数 (f) で表される数列:
a_i+1 = f(a_i)
は [code 2] の (inf-seq a0 f) で表されます。ここで、a0 は初項で、f は次の項を計算するための関数です。

(inf-seq a0 f) は再帰的な定義になっており、その定義から、初項が a0 第２項が (f a0) であり、第 n+1 項は (f a_n) で表されることが簡潔に表現されています。 inf-seq を使うと等差数列と等比数列はそれぞれ (ari a0 d), (geo a0 r) の様に定義できます。ここで、a0, d, r はそれぞれ初項、公差、公比を表します。

[code 2]

01:     ;;;;  sequences
02:     
03:     ;;; infinite sequences represented by a_(n+1) = f(a_n)
04:     (define (inf-seq a0 f)
05:       (lazy-cons a0 (inf-seq (f a0) f)))
06:     
07:     ;;;arithmetic sequence
08:     (define (ari a0 d)
09:       (inf-seq a0 (lambda (x) (+ x d))))
10:     
11:     ;;; geometric sequence
12:     (define (geo a0 r)
13:       (inf-seq a0 (lambda (x) (* x r))))

inf-seq で無限数列ができることを確認してみましょう（sample 2）。 geo を使って初項 1、公比 2 の等比数列 g1 と初項 1、公比 1/2 の等比数列 g2 を作り、head を使って最初の 10 項を表示させます。ちゃんと数列ができていることが確認されます。
次に、lazy-map を使って g1 と g2 を掛け合わせた数列を作り、 head で最初の 10 項を取り出します。1 が 10 個並び、ちゃんと計算されていることがわかります。

次に、等差数列と lazy-filter について調べてみましょう。まず、(ari 1 1) で、 (1 2 3 ....) という数列 ar1 を作ります。head で、最初の 10 項を表示させると 1 から 10 までが表示されました。さらに、lazy-filter を使って偶数を取り出し、最初の 10 項を表示させると 2 から 20 までが表示されます。

[sample 2]

> (define g1 (geo 1 2))         ;初項 1 公比 2 の等比数列
> (define g2 (geo 1 (/ 1 2)))   ;初項 1 公比 1/2 の等比数列
> (head g1 10)
(1 2 4 8 16 32 64 128 256 512)
> (head g2 10)
(1 1/2 1/4 1/8 1/16 1/32 1/64 1/128 1/256 1/512)
> (head (lazy-map * g1 g2) 10)
(1 1 1 1 1 1 1 1 1 1)
> (define ar1 (ari 1 1))        ;初項 1 公差 1 の等差数列
> (head ar1 10)
(1 2 3 4 5 6 7 8 9 10)
> (head (lazy-filter even? ar1) 10)
(2 4 6 8 10 12 14 16 18 20)

4.2.2 Fibonacci 数列

Fibonacci 数列は、

fib(1) = 1
fib(2) = 1
fib(n+1) = fib(n) + fib(n-1)

で表される数列です。lazy-cons と lazy-map を使うと、[code 3] に示す様に、数学上の定義のままのコードが書けます。しかも O(n) のオーダーで各項が計算されます。[sample 3] の値は瞬時に計算されます。

[code 3]

01:     (define fib
02:       (lazy-cons 1
03:                  (lazy-cons 1
04:                             (lazy-map + fib (lazy-cdr fib)))))

[sample 3]

> (head fib 20)
(1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765)
> (lazy-ref fib 100)
573147844013817084101

4.3. 無限数列の数値計算への応用

以下の例はなぜ関数プログラムは重要かにあった例を Scheme を使って書き直したものです。遅延評価の数値計算への応用については SICP 3.5. Streams も参照してください。

4.3.1. ニュートン-ラプソン法による平方根の計算

ニュートン-ラプソン法は数値 N の平方根を、初期近似値 a0 から始めて、以下の式を使って近似を良くしていく方法です。

     a(n+1) =  (a(n) + N/a(n)) / 2                   (2)

もし、この近似がある極限値 a に収束するなら、

      a =  (a +  N/a) / 2
したがって、
      2a = a +  N/a
      a =  N/a
      a*a = N
      a =  squareroot(N)

となり、確かに極限値 a は N の平方根です。 (2) 式より、次項は前項だけの関数なので、近似値の数列は inf-seq で表せます。初期値は 1 に固定しましたが、この数列は収束が早いので問題はありません。

[code 4] に平方根を求めるプログラムを示します。

[code 4]

01:     ;;; Newton-Raphson method
02:     (define (newton-raphson n)
03:       (inf-seq 1 (lambda (x) (/ (+ x (/ n x)) 2))))
04:     
05:     ;;; returning a reasonable answer.
06:     ;;; If the ratio of successive terms is in (1 - eps) and (1 + eps),
07:     ;;; or the following term is zero,
08:     ;;; the function returns it.
09:     (define (lazylist->answer ls eps)
10:       (let ((e1 (- 1.0 eps))
11:             (e2 (+ 1.0 eps)))
12:         (let loop ((val (lazy-car ls))
13:                    (ls1 (lazy-cdr ls)))
14:           (let ((val2 (lazy-car ls1)))
15:             (if  (or (zero? val2) (< e1 (/ val val2) e2))
16:                 (exact->inexact val2)
17:               (loop val2 (lazy-cdr ls1)))))))
18:     
19:     ;;;
20:     (define (my-sqrt n eps)
21:       (lazylist->answer (newton-raphson n) eps))

(newton-raphson n): n の平方根の近似値の遅延リストを作る関数です。
(lazylist->answer ls eps): 遅延リストの連続する２項の比が (1 - eps) と (1 + eps) との間に入るか、２番目の項がゼロになれば、その２番目の項を返します。
(my-sqrt n eps): n の平方根を相対誤差 eps で求めます。

> (my-sqrt 9 0.0000001)
3.0

4.3.2. 数値微分

単純な微分の式は [code 5] の easydiff で表されます。この式で f は微分を求める関数、 x は微分を求める x の値、 h は微分を求めるための x の値の幅です。理論上は h をゼロに近づければ微分の値の近似は良くなりますが、コンピュータの数値計算上の誤差が生ずるため h をあまり小さくはできません。

そこで、lazylist-diff に示すように初期値 h0 から初めてその値を半分にしていく遅延リスト (geo h0 0.5) を作り、それに対応する近似値の微分リストを作ります。

(lazylist->answer (lazylist-diff h0 f x) eps)

を使って素直に値を求めても良いのですが、収束が遅いので、収束を早くする関数 super を使って収束を早めます。収束を早めるテクニックについてはなぜ関数プログラミングは重要かを見てください。収束を加速させるアルゴリズムはそれなりに複雑で、通常の反復を使ったコーディングではかなりの量になります。遅延評価を使うとそれが、数学の定義に近い形で簡潔に表現できます。また、プログラムがモジュール化されているのでそのまま他の問題に適応できます。4.3.3. 節で示す数値積分は [code 5] で示した収束加速関数をそのまま再利用しています。

[code 5]

01:     ;;; differentiation
02:     
03:     ;;; primitive function for differentiation
04:     (define (easydiff f x h)
05:       (/ (- (f (+ x h)) (f x)) h))
06:     
07:     ;;; create a lazy list of approximation for differentiation
08:     (define (lazylist-diff h0 f x)
09:       (lazy-map (lambda (h) (easydiff f x h)) (geo h0 0.5)))
10:     
11:     ;;; eliminate error from the approximation
12:     (define (elimerror n ls)
13:       (let ((a (lazy-car ls))
14:             (b (lazy-second ls))
15:             (c (expt 2 n)))   
16:         (lazy-cons
17:          (/ (- (* b c) a) (- c 1))
18:          (elimerror n (lazy-cdr ls)))))
19:     
20:     ;;; estimate `n' in elimerror
21:     (define (order ls)
22:       (let* ((a (lazy-car ls))
23:              (b (lazy-second ls))
24:              (c (lazy-ref ls 2))
25:              (d (- (/ (- a c) (- b c)) 1.0)))
26:         (cond
27:          ((< d 2) 1)
28:          ((<= 2 d 16) (inexact->exact (round (log2 d))))
29:          (else 4))))
30:     
31:     ;;;
32:     (define (log2 x)
33:       (/ (log x) (log 2)))
34:     
35:     ;;; improve convergency of the lazy list of the approximation
36:     (define (improve ls)
37:       (elimerror (order ls) ls))
38:     
39:     ;;; return the second value of the lazy list
40:     (define (lazy-second ls)
41:       (lazy-car (lazy-cdr ls)))
42:     
43:     ;;; further improve the convergency of the list
44:     (define (super ls)
45:       (lazy-map lazy-second (inf-seq ls improve)))
46:                 
47:     
48:     ;;; calculate the differentiation of function `f' at x within error eps
49:     ;;; h0 is initial window width
50:     (define (diff f x h0 eps)
51:       (lazylist->answer (super (lazylist-diff h0 f x)) eps))

> (diff sin 0.0 0.1 0.0000001)
0.9999999999999516
> (diff exp 0.0 0.1 0.000001)
0.9999999991733471

4.3.3. 数値積分

収束を早めるためのテクニックはそのまま数値積分にも使えます。まず、easyintegrate でごく荒い近似を定義します。それを区間の中点で区切って近似を上げていく遅延リスト lazylist-integrate を定義します。この関数は再帰関数で、lazy-map を使って簡潔に書くことができます。最後に関数 integrate で数値微分の場合と同様に収束を加速し、収束した値を返します。

実行例に示すように正常に動作します。

[code 6]

01:     ;;; integration
02:     
03:     ;;; primitive integration
04:     (define (easyintegrate f a b)
05:       (* (/ (+ (f a) (f b)) 2) (- b a)))
06:     
07:     ;;; create the lazy list of approximation for integration
08:     (define (lazylist-integrate f a b)
09:       (let ((mid (/ (+ a b) 2)))
10:         (lazy-cons (easyintegrate f a b)
11:                    (lazy-map + (lazylist-integrate f a mid)
12:                                (lazylist-integrate f mid b)))))
13:     
14:     ;;; integrate function `f' in a range of `a' and `b' within error `eps'
15:     (define (integrate f a b eps)
16:       (lazylist->answer (super (lazylist-integrate f a b)) eps))

> (integrate sin 0 pi 0.0000001)
2.000000002272428
> (integrate exp 0 1 0.0000001)
1.7182818277724858
> (- (exp 1) 1)
1.718281828459045

5. 終わりに

遅延評価を用いるとデータ構造に繰り返しを自然に組み込むことができます。

通常のプログラム言語では繰り返しはそれ用の構文を使って書く必要があったのでプログラムのモジュール化には限界があります。一方、遅延評価リストを使うとデータに繰り返し計算されるという性質を持たせることができるので、プログラムを簡潔に書くことができます。

遅延評価についてさらに詳しく知りたい人は Haskell 関連のページを google で探ってみてください。よろしかったら拙作 Haskell のお勉強も見てみてください。

このページで示したコードは付録につけておきますので気が向いたらダウンロードして遊んでみてください。