HOME Common Lisp download 書き込む

フラクタル曲線を描く

1. はじめに

フラクタル曲線は再帰的に定義されるので、再帰関数を多用する LISP にはうってつけの課題です。 ここでは、clisp と gnuplot を使って C 曲線、ドラゴン曲線、ヒルベルト曲線を描きます。 ソースを見ていただくと分かるように非常に短いコードで書くことが出来ます。 また、実行時間も 10 秒以内 (Pentium II 300MHz) ですみます。

LISP は AI 向けの言語と言われていますが、数値計算も得意分野の一つです。 実際、数値を扱うプログラムを書くことは非常に容易です。

計算結果を gnuplot を使って表示する方法が皆様の参考になれば幸いです。

2. 準備

gnuplot をインストール必要があります。gnuplot は高性能なフリーのプロットソフトで 広く利用されています。もちろん Win32 版もあり簡単にインストールできます。

2.1. gnuplot のインストール

gnuplot はsourceforge.net から、ダウンロード出来ます。gp400win32.zip (7 月 1 日現在）をダウンロードして適当なディレクトリに 解凍してください。/bin の中にある。wgnuplot.exe をダブルクリックするとコンソールが現れます。 表示が小さくて読めないときはマウスコンソール上で右ボタンを押すと choose font というメニューが 現れますので、それをクリックしてフォントサイズを大きくして下さい（例えば 14 pt）。 表示の変更は Update Wgnuplot.ini を選択して保存しておきます。 コンソールから plot sin (x) と入力してみてください。 サインカーブが描かれるはずです。詳しい使い方は付属の help または、 gnuplot homepageを参考にしてください。 日本語のページでは、 などが比較的新しい情報を取り入れています。

wgnuplot.exe と同じディレクトリに入っている pgnuplot.exe は、他のプログラムから gnuplot にコマンドを渡すのに使います。

環境変数 GDFONTPATH をフォントのあるディレクトリ（例えば、"C:\WINDOWS\FONTS\"）に設定しておくと png ファイル (portable network graphics) にイメージを書き出すときにそのディレクトリにある TrueType (*.ttf) フォントと Adobe Type 1 (*.pfa) フォントが使用できます。

2.2. fractal.lisp のインストール

ダウンロードした fractal.lzh を適当なディレクトリで解凍します。 エディタでソース (fractal.lisp) を開いて、(mark 1) のコメントが入っている行の *gnuplot* を自分の pgnuplot にあわせて書き換えます。 wgnuplot.exe ではなく pgnuplot.exe です。くれぐれもお間違いのないようにして下さい。 その部分の書き換えが済んだら clisp を立ち上げて、コンパイルした後、ロードします。 （ちなみに、Linux 上で動かすときは pgnuplot ではなく、gnuplot を指定してください。）

> (compile-file "fractal.lisp")
> (load "fractal")

3. fractal.lisp の使用法

3.1. テスト

gplot が gnuplot にコマンドを渡す関数です。この関数は文字列を引数に取ります。例えば

> (gplot "plot sin (x)")
と入力してみてください。サインカーブが描かれればインストールは成功です。

以下に gnuplot を操作する関数を挙げます。

(gplot string)
gnuplot に string のコマンドを送ります。改行文字は入れないでください。
(auto)
autoscale にして replot します。
(range xmin xmax ymin ymax)
x-range, y-range を入力した値にして replot します。 数値以外の値を引数に与えると range は変化しません。
例えば、(range -2 2 nil nil) は x-range だけが変化します。
(png filename)
png ファイルにイメージを書き出し、gnuplot を終了して、再起動します。 （終了しないとファイルが閉じないため）filename は拡張子無しで与えます。環境変数 GDFONTPATH が設定してあるとフォントは *png-font-type* と *png-font-size* で設定したものになります。 （ソースコードの (mark 1a) (mark 1b) を見て下さい。） 設定してなければ gnuplot のデフォルトになります。
(end-plot)
gnuplot を終了します。
そのほかに必要な関数があれば、ソースコードの (mark 3) を参考にして作ってみてください。

3.2. C 曲線、ドラゴン曲線を描く

C 曲線、ドラゴン曲線 は直線を９０度ずつ折り曲げていったときに出来る曲線です。同じ向きに折り曲げると C 曲線、 交互に違う向きに折り曲げるとドラゴン曲線になります。 詳しい説明は 再帰曲線で遊ぼう にあります。また、次のサイトにも説明があります。 fractal.lisp にC 曲線、ドラゴン曲線を描かせるには、clisp のコマンドプロンプトから 
> (c-curve '((x1 y1)(x2 y2)) n)
> (dragon '((x1 y1)(x2 y2)) n)
と入力してください。ここで、(x1 y1) (x2 y2) は初期座標、n は繰り返しの回数です。 図１、２に示すような図がえられます。

図１：C 曲線

図２：ドラゴン曲線

3.3. ヒルベルト曲線を描く

ヒルベルト曲線は、連続した曲線で平面を覆う曲線の一つです。 詳しい説明は 再帰曲線で遊ぼう、 や Example of recursion: Hilbert Curvesにあります。 fractal.lisp にヒルベルト曲線を描かせるには、clisp のコマンドプロンプトから 
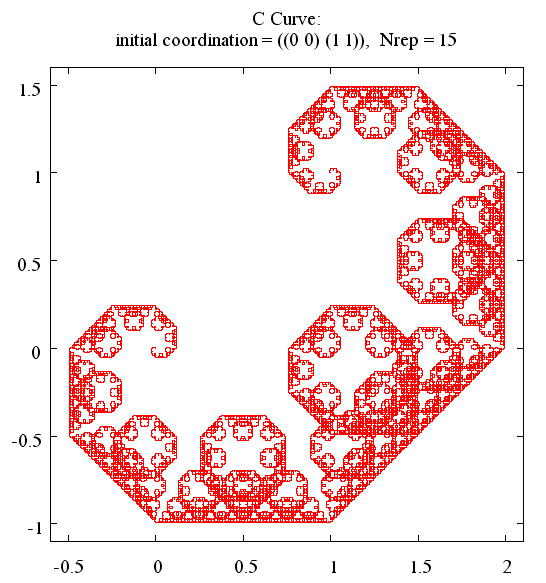
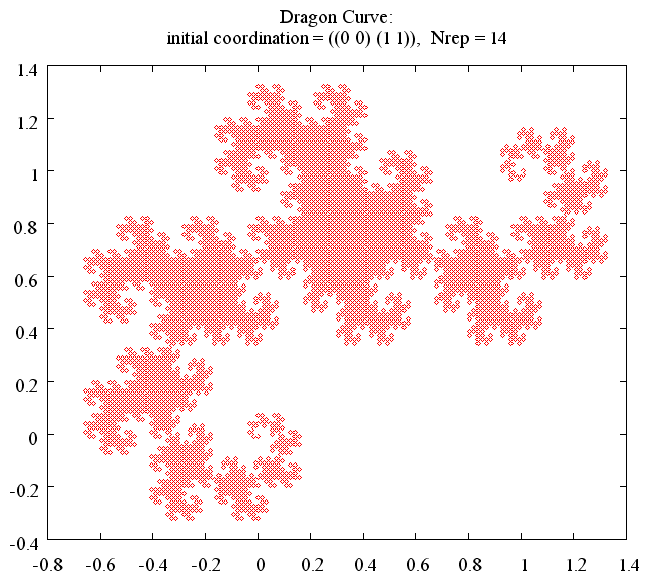
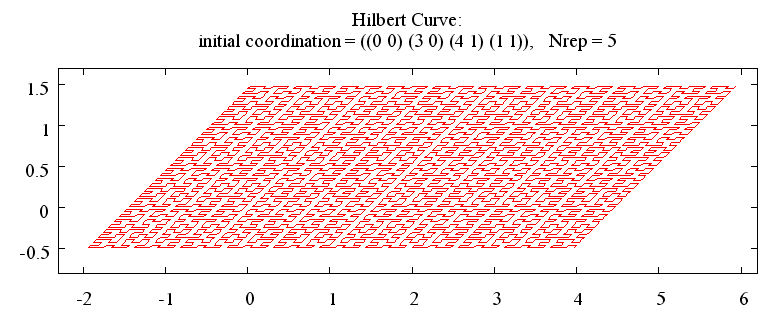
> (hilbert '((x1 y1) (x2 y2) (x3 y3) (x4 y4)) n)
と入力してください。ここで、(xi yi) (i = 1 ∼ 4) は初期座標、n は繰り返しの回数です。 初期座標には平行四辺形を与えてください。 もちろん、正方形、長方形、ひし形を含みます。位置や方向は問いません。 図３〜５に示すような図がえられます。

図３：ヒルベルト曲線（正方形、座標軸に直行）

図４：ヒルベルト曲線（ひし形）

図5：ヒルベルト曲線（平行四辺形）

4. 解説

4.1. gnuplot との接続

gnuplot にコマンドを送るには次の様な関数を使います。 この関数は pipe 名とディレクトリ名を覚えていて（注１）、pipe がつながっていれば それを使い、つながっていなければ新たにつなげます(mark 3a)。 （つまり、png ファイルを 作成するとき gnuplot を閉じても必要なときに自動的に立ち上がります。） また、ディレクトリが 変わったら、"cd" コマンドを gnuplot に送ります (mark 3b)。 コマンドを送る部分は (mark 3c) の部分です。まず、pipe に対して format 関数で 出力してから (format gp "~A~%" s)、バッファーを 強制的に吐き出し(force-output gp)、pgnuplot に 命令を送ります。 また、"exit" 命令が入力されたら、それを pgnuplot に送った後 pipe を閉じます。 
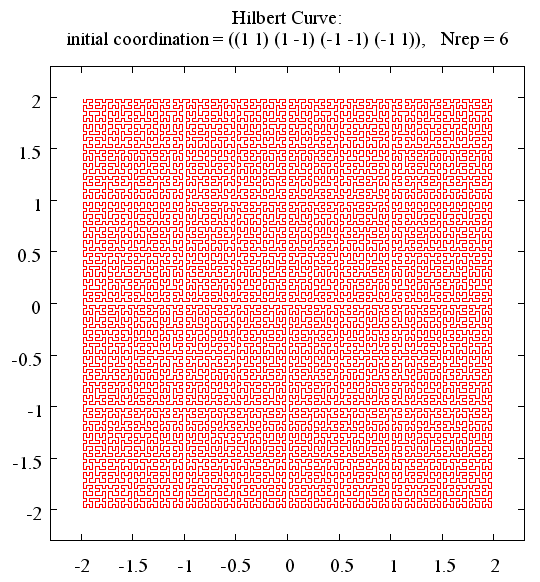
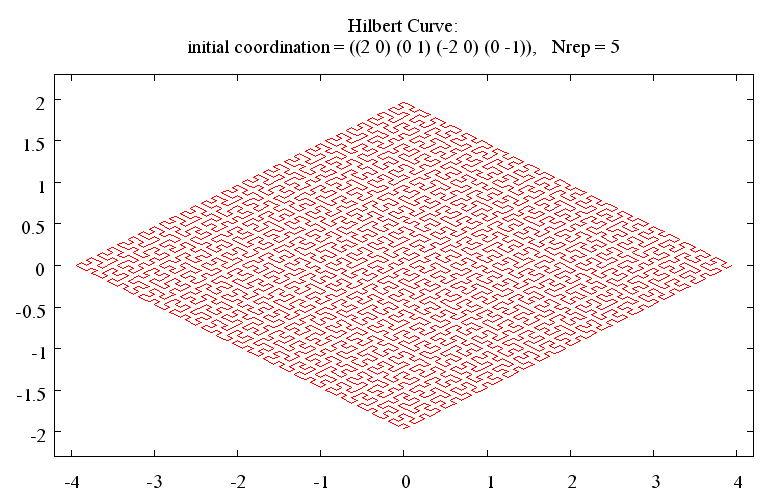
;;; send command to gnuplot                ; (mark 3)
(let (gp dir)
  (defun gplot (s)
    (or gp
	(setq gp (make-pipe-output-stream *gnuplot* :buffered t)))  ;(mark 3a)
    (or dir                                                          ;(mark 3b)
	(setq dir (ext:cd)))
    (let ((dir1 (ext:cd)))
      (unless (equal dir dir1)
	(setq dir dir1)
	(format gp "cd \'~A\'~%" (string-right-trim "\\" (format nil "~A" dir)))
	(force-output gp)))
    (when (stringp s)
      (format gp "~A~%" s)                                           ;(mark 3c)
      (force-output gp)
      (when (string-equal s "exit")                                  ;(mark 3d)
	(close gp)
	(setq gp nil)))))
注１：この関数はクロージャー (let (gp dir) ........)で囲まれているので、 呼び出し終了後も変数 gp, dir を保持できます。詳しいことは 堀井氏の解説 を読んでください。

4.2. LISP の構造体

リスプの構造体は defstruct で定義します。このスクリプトでは２次元の点を表す構造体 "v" を 定義しています。構造体についての詳しいことは 堀井氏の解説 を見てください。C や Fortran では配列を使うところですが、LISP では配列より構造体の方が便利です。 
(defstruct v (x 0.0 :type single-float) (y 0.0 :type single-float))                         ; (mark 2)
構造体 "v" のスロットはそれぞれ x 座標 y 座標を表す x, y の２つです。スロットのタイプを 指定しておくと計算が速くなります。構造体を定義すると、 それに付随する関数も自動的に定義されます（注２）。この例では以下の４つの関数が定義されます。
make-v
構造体 "v" を作ります。
v-x
スロット x にアクセスします。
v-y
スロット y にアクセスします。
v-p
ある変数が構造体 "v" かどうか調べます。
この構造体を使ってベクトル演算をする関数 v+, v-, v* やその他の関数を定義します。 これらの関数を使うと座標を扱うプログラムが簡潔に書けます。
;;;;;;;;;;;;;;; functions for 2D vectors  ;;;;;;;;;;;;;;;;;;;;;;; (mark 4)
;;; add vectors
(defun v+ (&rest argvs)
  (make-v :x (apply '+ (mapcar #'v-x  argvs))
          :y (apply '+ (mapcar #'v-y  argvs))))

;;; subtract vectors
(defun v- (&rest argvs)
  (make-v :x (apply '- (mapcar #'v-x  argvs))
          :y (apply '- (mapcar #'v-y  argvs))))

;;;multiplication or inner product 
(defun v* (v0 n)
    (make-v :x (* (v-x v0) n)
            :y (* (v-y v0) n)))

;;; convert initial input to  structure v
(defun l2v (ls0)
  (make-v :x (coerce (first ls0) 'single-float) :y (coerce (second ls0) 'single-float)))

;;; calculating center
(defun vcl (ls0)
  (let ((n (length ls0)))
    (make-v :x (/ (apply '+ (mapcar #'v-x ls0)) n)
            :y (/ (apply '+ (mapcar #'v-y ls0)) n))))
注２：LISP には macro という機能があり、プログラムを自動で生成することが出来ます。 詳しくは 堀井氏の解説 を見てください。

4.3 c-curve について

最後に、実際にフラクタル曲線を生成する関数を c-curve を例にとって説明します。 下の囲みにソースを示します。LISP を使うとソースがとても短くなるのが分かります。

マクロ c-gen は v1, v2 を底辺とする 直角二等辺三角形の頂点の位置ベクトルを求めます (a)。必ずインライン展開されるように マクロで定義しました。

c-curve が本体の関数です。 実行速度を上げるために (optimize (speed 3) (safety 0)) の宣言をします (b0)。 C-curve の点の総数は、繰り返し回数 n から、 2n + 1 で求まります。そこで、全ての点を格納できる配列 *fractal-array* を作り (b1)、 初期座標を配列の両端にセットします (b2, b3)。 次に、間の点を i を 0 から (n - 1) まで増やして 順番に埋めていきます(c1)。 i 番目のときの配列のインデックスの間隔 d は (c2) で求まります。新しく追加する点のインデックス idx は配列の最後のインデックス asize0 より小さい間 d から 2d ずつ 増加していきます(c3)。 新しく求める点の座標はインデックス (idx - d), (idx + d) の座標から c-gen を用いて求めます(c4)。 これを i = (n - 1) まで繰り返すと、配列はだんだんつまっていき、 最後に全部埋まります。

そうなったら、 plot-c/dragon を使ってプロットします (d1)。 plot-c/dragon は、まず、 配列 *fractal-array* の要素を *fractal-data-file* に書き出し (e1)、さらにプロット用 コマンドファイル *fractal-plot-file* をつくり (e2)、それを gnuplot にロードさせます (e3)。gnuplot がプロットしている間に、 *fractal-array* に nil をセットし (e4)、不要になったメモリー を開放します (e5)。配列を使うと、リストを使って繰り返し計算するよりゴミが少ないという利点が あります。また、計算速度も速くなります。

;;; generate points for c curve              ; a
(defmacro c-gen (v1 v2)
  (let ((gv1 (gensym)) (gv2 (gensym)))
    `(let ((,gv1 ,v1) (,gv2 ,v2))
       (make-v :x (* 0.5e0 (+ (v-x ,gv1) (v-x ,gv2) (- (v-y ,gv2) (v-y ,gv1))))
               :y (* 0.5e0 (+ (v-y ,gv1) (v-y ,gv2) (- (v-x ,gv1) (v-x ,gv2))))))))

;;; making a C curve, (c-curve '((x1 y1) (x2 y2)) n)  ; b      
(defun c-curve (ini n)
  (let* ((asize0 (expt 2 n))
         (asize (1+ asize0)))
    (declare (optimize (speed 3) (safety 0)))                                    ; b0
    (setf *fractal-array*                    (make-array asize :element-type 'v) ; b1
          (svref *fractal-array* 0)          (l2v (first ini))                   ; b2
          (svref *fractal-array* asize0)     (l2v (second ini)))                 ; b3
    (dotimes (i n)                                                               ; c1
      (let* ((d (expt 2 (- n i 1)))                                              ; c2
             (d2 (* 2 d))
             (idx (* -1 d))) 
        (while (< (incf idx d2) asize0)                                          ; c3
          (setf (svref *fractal-array* idx)                                      ; c4
		(c-gen (svref *fractal-array* (- idx d))
		       (svref *fractal-array* (+ idx d)))))))
  (plot-c/dragon "C" asize ini n)))                                              ; d1

;;; plotting the result of calculation of C/dragon
(defun plot-c/dragon (type asize ini n)
  (with-open-file (out *fractal-data-file* :direction :output)                   ; e1
    (dotimes (i asize)
      (format out "~A ~A~%" (v-x (svref *fractal-array* i)) (v-y (svref *fractal-array* i)))))
  (with-open-file (out *fractal-plot-file* :direction :output)                   ; e2
    (format out "set title \"~A Curve:\\ninitial coordination = ~S,  Nrep = ~D\"~%" type ini n)
    (format out "set key off~%")
    (format out "set size square~%")
    (format out "set size ratio -1~%")
    (format out "set autoscale~%")
    (format out "plot \"~A\" w l 1~%" *fractal-data-file*))
  (gplot (format nil "load \"~A\"" *fractal-plot-file*))                          ; e3
  (nilf *fractal-array*)                                                          ; e4
  (sleep (* asize 0.0001))
  (gc)                                                                            ; e5
  t)

5. おわりに

今回はフラクタル曲線を例にとって clisp で行った計算結果を gnuplot で表示させる方法について 説明しました。実行していただくと分かるように、計算時間は C や Fortran で書いたものとそれほど 変わりません。LISP で書くとプログラムコードの長さは C や Fortran の 1/10 位なので、慣れれば LISP を使うのは非常に有利です。例えば、LISP で書けば、作成に 6 時間、実行に 10 時間、 一方、C や Fortran で書けば作成に 3 日、実行に 5 時間だとすると、LISP を使えば翌日（コンピューターは 寝ずに働く）結果が得られるのに対し、C や Fortran では週末までかかることになります。 数値計算の分野でも LISP が普及するのを願います。（正直に言うと、残念なことにどの分野でも LISP は あまり普及していません。LISP が優れた言語であるにもかかわらず。）LISP が優れた言語であることは NASA のレポートにもあります。 また Paul Graham のホームページも見て下さい。

HOME Common Lisp download 書き込む