HOME
8. Monad
Haskell のお勉強
10. 種々のデータ構造
download
書き込む
|
HOME |
8. Monad |
Haskell のお勉強 |
10. 種々のデータ構造 |
download |
書き込む |
探索のアルゴリズムには大きく分けて、深さ優先探索 (depth first search) と 幅優先探索 (breadth first search) の２つがあります。
深さ優先探索とは、終点にたどり着くか、行き止まりになるまで１つの経路を探索してから、 次の経路を探索する方法です。プログラムが簡単なのと、メモリー量、計算時間が比較的短くて済むという 特徴があります。ただし、最初に見つかった経路が最短経路だという保障はありません。 行き止まりになったら元の地点に戻って他の可能性を探すことをバックトラックといいます。
それに対し、幅優先探索とは、全ての可能性について一様に探索する手法です。 メモリーを消費し、比較的計算時間が長くかかりますが、 最初に見つかった経路が最短であることが保障されています。
また、両方の手法で、一度訪れた節を再び訪れないようにする必要があります。 そうしないとループにはまってしまいます。
深さ優先探索のコードを以下に示します。
[code 1]
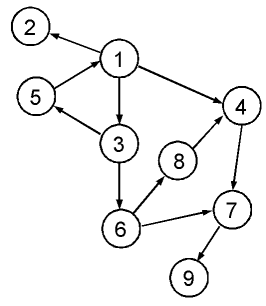
01: -- easy search 02: 03: module EasySearch where 04: 05: import Monad 06: 07: type Graph = ([Int], [(Int, Int)]) 08: 09: -- graph with loop 10: gr0 :: Graph 11: gr0 = ( [1,2,3,4,5,6,7,8,9], -- nodes 12: [(1,2),(1,3),(1,4),(2,5),(3,5),(3,6),(4,7),(5,1),(6,7),(6,8),(7,9),(8,4)]) -- arrows 13: 14: find_next :: Int -> Graph -> [Int] 15: find_next k gr = map snd $ filter ((==k) . fst) (snd gr) 16: 17: -------------------------------------------------------------------------- 18: -- depth first search 19: --dfs :: Graph -> Int -> Int -> Maybe [Int] 20: dfs :: Graph -> Int -> Int -> [[Int]] 21: dfs gr p0 p1 = dfs_aux gr p0 p1 [] 22: 23: dfs_aux gr p0 p1 path 24: | p0 == p1 = return (reverse (p1:path)) 25: | otherwise = msum $ 26: map (\p -> dfs_aux gr p p1 (p0:path)) 27: [ x | x <- find_next p0 gr, not (x `elem` path)][図 1]
| 行 | 説明 |
|---|---|
| 5 | module Monad を import しています。このことによって class MonadPlus が使えるようになります。 |
| 7 | ([Int], [(Int, Int)]) に Graph という別名をつけます。 以降、([Int], [(Int, Int)])と書く代わりに Graph と書くことが出来ます。Graph は [Int], [(Int, Int)] の２つのリストからなる pair で、最初のリストは節、２番目は辺のリストです。 |
| 10--13 | 図１に示す構造を持つ有向グラフを定義します。 |
| 14--15 | find_next は gr に含まれる節 k に隣接する節のリストを返します。 |
| 16--19 | 深さ優先探索を行う関数 dfs の型宣言です。Maybe [Int] を返すか、 [[Int]]を返すか選ぶことが出来ます。 |
| 21 | dfs の定義があります。補助関数 dfs_aux を使って定義されています。 |
| 23--27 | dfs_aux の定義です。dfs_aux の型宣言は明示的に行わず、処理系に任せます。 |
| 23 | dfs_aux は４つの引数をとります。最初から順番に、グラフ (gr)、現在の節 (p0)、目的の節 (p1)、（降順の）たどってきた経路 (path) です。 |
| 24 | もし、現在の節が目的の節と等しければ、経路 (reverse (p1:path)) を返します。 |
| 25 | そうでなければ、p0 に隣接する節で、まだ、訪れていないもの ([ x | x <- find_next p0 gr, not (x `elem` path)]) のリストについて深さ優先探索 (dfs_axu) を map し、その結果を msum します。 |
msum :: MonadPlus m => [m a] -> m a msum xs = foldr mplus mzero xsmzero, mplus の定義は以下の通りです。
-- Instances of MonadPlus
instance MonadPlus Maybe where
mzero = Nothing
Nothing `mplus` ys = ys
xs `mplus` ys = xs
instance MonadPlus [] where
mzero = []
mplus = (++)
msum は以下のような動作をします。
msum [Nothin, Just 1, Just 2] ⇒ Just 1 msum [[], [1], [2]] ⇒ [1, 2]実行結果を以下に示します。dfs が Maybe [Int] を返す型の場合は最初に見つかった経路が、 [[Int]] の場合は全ての経路が返ってきます。 [code 1] の 19, 20 行目を入れ替えるだけで 得られる結果を変えることが出来ます。
-- dfs :: Graph -> Int -> Int -> Maybe [Int] のとき EasySearch> dfs gr0 1 9 Just [1,3,6,7,9] -- 最初に見つかった経路を返す。 -- dfs :: Graph -> Int -> Int -> [[Int]] のとき EasySearch> dfs gr0 1 9 [[1,3,6,7,9],[1,3,6,8,4,7,9],[1,4,7,9]] -- 見つかった経路全てのリストを返す。
[code 2]
01: -- breadth first search 02: bfs :: Graph -> Int -> Int -> [[Int]] 03: --bfs :: Graph -> Int -> Int -> Maybe [Int] 04: 05: bfs gr p0 p1 = bfs_aux gr p1 [ x : [p0] | x <- find_next p0 gr] 06: 07: bfs_aux _ _ [] = fail "no path" 08: bfs_aux gr p1 (path:queue) 09: | p0 == p1 = (return (reverse path)) `mplus` (bfs_aux gr p1 queue) 10: | otherwise = bfs_aux gr p1 ( queue ++ 11: [ x : path | x <- find_next p0 gr, not (x `elem` path)]) 12: where p0 = head path2,3 行目で幅優先探索を行う関数 bfs の型を宣言します。
実行例を以下に示します。dfs の場合と同様に、 bfs の型によって、返る値が違ってきます。
-- bfs :: Graph -> Int -> Int -> Maybe [Int] のとき EasySearch> bfs gr0 1 9 Just [1,4,7,9] -- 最短経路を返す。 -- bfs :: Graph -> Int -> Int -> [[Int]] のとき EasySearch> bfs gr0 1 9 [[1,4,7,9],[1,3,6,7,9],[1,3,6,8,4,7,9]] -- 見つかった経路全てのリストを短い順に返す。これらのことから、Monad を使えば、Maybe 型と List 型は全く同じに取り扱える ことが分かります。つまり、List の Monad が定義されていることによって、 コードの再利用が促進されます。
一般に川渡り問題というのは、 ２人乗り（N>2 人乗りの場合もある）のボートを用いて、許されない組み合わせを回避しながら全員を対岸に渡す際の 最短経路を求める問題です。
三夫婦の川渡り問題の場合は、夫がいないときに妻が他の男といるのは許されないと いう制約がつきます。
最短経路を求める問題なので、幅優先探索で解くことにします。 プログラムを容易にするために、３人の夫に正の整数 1,2,3 の、 彼らの妻に絶対値が等しい負の整数 -1, -2, -3 の番号をつけます。
さらに、３組の夫婦が等価であることを利用して探索する局面の 数を減らします。３組の夫婦は等価なので、岸の状態は、夫の人数、妻の人数、夫婦の数、 ボートの有無のみで区別され、どの夫婦がいるかは経路を求める際に考慮する必要はありません。 data 型 River を定義し、 上で述べた方針で River の Eq を定義します。こうすると 探索する局面の数が著しく減少します。
コードを以下に示します。
[code 3]
01: --------------------------------------------------------------------------- 02: -- river_cross.hs 03: -- by T.Shido (shido_takafumi@ybb.ne.jp) 04: -- 05: -- Getting one of the shortest path for the river crossing puzzle of three couples: 06: -- three couples are going to cross a river using a boat under following conditions. 07: -- 1) the boat is two-seated 08: -- 2) All wives should be with their husbands if other men are with them. 09: -- 10: -- In this program, the husbands are represented by 1, 2, and 3, and 11: -- their wives are by -1, -2, and -3. 12: ----------------------------------------------------------------------------- 13: 14: module Main where 15: 16: import List 17: 18: data River = River { 19: this :: [Int], -- the river side where people are at the beginning 20: that :: [Int], -- the river side where people are at the end 21: boat :: Bool -- if the boat is at `this' 22: } deriving Show 23: 24: -- 25: instance Eq River where 26: r1 == r2 = n_hus this1 == n_hus this2 && 27: n_wif this1 == n_wif this2 && 28: n_cop this1 == n_cop this2 && 29: boat r1 == boat r2 30: where this1 = this r1 31: this2 = this r2 32: 33: ---- 34: n_hus :: [Int] -> Int 35: n_hus = length . (filter (>0)) 36: 37: n_wif :: [Int] -> Int 38: n_wif = length . (filter (<0)) 39: 40: n_cop :: [Int] -> Int 41: n_cop [] = 0 42: n_cop (x:xs) = (if (negate x) `elem` xs then 1 else 0) + n_cop xs 43: 44: --- 45: remove_couple :: [Int] -> [Int] 46: remove_couple [] = [] 47: remove_couple (x:xs) = if elem x' xs 48: then remove_couple (delete x' xs) 49: else x : (remove_couple xs) 50: where x' = negate x 51: 52: --- check if the river situation is safe 53: safe :: River -> Bool 54: safe' :: [Int] -> Bool 55: 56: safe river = safe' (this river) && safe' (that river) 57: safe' ls = all (<0) ls || all (>0) (remove_couple ls) 58: 59: --- breadth first search for river crossing 60: river_bfs :: [River] -> [[River]] -> [River] 61: river_bfs _ [] = [] 62: river_bfs track (path:qs) 63: | this now == [] = reverse path 64: | otherwise = river_bfs (now:track) 65: (qs ++ [ next:path | next <- update_river now, next `notElem` track]) 66: where now = head path 67: 68: --- return the list of possible situation 69: update_river :: River -> [River] 70: update_river = nub . (filter safe) . choices 71: 72: --- return the list of next river situation 73: choices :: River -> [River] 74: choices river = [ River{ 75: this = (if boat river then (\\) else (++)) (this river) x, 76: that = (if boat river then (++) else (\\)) (that river) x, 77: boat = not (boat river)} 78: | x <- group ls0 ++ -- x is people who ride boat. 79: filter safe' [[x, y] | x <- ls0, y <- (fst . (break (==x))) ls0]] 80: where ls0 = (if boat river then this else that) river 81: 82: --- 83: main :: IO() 84: main = mapM_ print (river_bfs [] [[River{ this = [-3,-2,-1,1,2,3], 85: that = [], 86: boat = True }]])簡単な説明
| 行 | 説明 |
|---|---|
| 14 | module List を import する。List 用の種種の関数が使えるようになる。 |
| 18--22 | data River を名前付きフィールドを用いて定義する。 this は初めの岸にいる人のリスト、that は向こう岸にいる人のリストboat はボートが 初めの岸にあれば True。 |
| 25--31 | data River の Eq を定義する。this の夫、妻、夫婦の数が等しく、boat が 等しければ２つの River は等しい。 |
| 34--35 | 夫の数を求める。 |
| 37--38 | 妻の数を求める。 |
| 40--42 | 夫婦の数を求める。 |
| 45--50 | リストから夫婦を取り除いたリストを返す。 remove_couple [-1,1,2,3] ⇒ [2,3] |
| 54,57 | 引数が許容される組み合わせであるか調べる。許容されれば True |
| 53,56 | River が許容される常態か調べる。 |
| 60--66 | 幅優先探索を行う。最短経路を返すだけなら Monad を使う必要はない。 river_bfs は探索した局面のリスト (track) と経路の待ち行列の ２つの引数を取る。待ち行列が [] なら [] を返す。 待ち行列が (path:qs) なら、
|
| 69--70 | River の局面から次の可能な局面を生成して返す。 まず、choices でボートを動かすことによって生成する全ての局面を生成し、 それを safe を使って filtering する。さらに、nub で等価な局面を取り除く。 |
| 73--80 | ボートを動かすことによって生成する全ての River を返す。
ボートが初めの岸にあれば、this から、向こう岸にあれば that から
許容される組み合わせの１人か２人選んで対岸に渡す。 (\\) は２つの引数の差集合を返す。 [1,2,3] \\ [1] ⇒ [1,2] group は引数の要素をリストにして返す。 group [1,2,3] ⇒ [[1], [2], [3]] つまり、group ls0 はボートに１人乗っている場合、 filter safe' [[x, y] | x <- ls0, y <- (fst . (break (==x))) ls0] はボートに２人乗っている場合である。 |
| 83--86 | main 関数。mapM_ print で結果を表示。 |
実行例: 11 ステップで渡河が完了します。
D:\doc\05-04\hs>runhugs river_cross.hs
River{this=[-3,-2,-1,1,2,3],that=[],boat=True} -- initial, step 0
River{this=[-3,1,2,3],that=[-1,-2],boat=False}
River{this=[-2,-3,1,2,3],that=[-1],boat=True}
River{this=[1,2,3],that=[-3,-2,-1],boat=False}
River{this=[-1,1,2,3],that=[-3,-2],boat=True}
River{this=[-1,1],that=[3,2,-3,-2],boat=False}
River{this=[-2,2,-1,1],that=[3,-3],boat=True}
River{this=[-2,-1],that=[1,2,3,-3],boat=False}
River{this=[-3,-2,-1],that=[1,2,3],boat=True}
River{this=[-3],that=[-1,-2,1,2,3],boat=False}
River{this=[-2,-3],that=[-1,1,2,3],boat=True}
River{this=[],that=[-3,-2,-1,1,2,3],boat=False} -- final, step 11
気が向いたら、このプログラムを改造して、
宣教師と人食い人種版を作ってみてください。
禁制条件がシンプルなのでプログラムはむしろ短くなります。
探索問題については
などを見てください。また、 川渡り問題については
を見て下さい。|
HOME |
8. Monad |
Haskell のお勉強 |
10. 種々のデータ構造 |
download |
書き込む |