6. Haskell で最小二乗法

前回までの知識で普通のプログラムを書くことが出来るようになったので、今回は復習を兼ねて線形最小二乗法のプログラムを書いてみました。

1. 線形最小二乗法のおさらい

線形最小二乗法をごく簡単におさらいします。ちゃんと知りたい人は google などで検索してください。

(x,y) の測定値の対を N 回測定したとします。ここで、x の値は正確で y の値にだけ誤差が含まれているとします。このデータを
y = c₀ + c₁ x + c₂ x² ...+ c_D x^D
という D 次の線形多項式でフィットし、係数
c₀, c₁, c₂ .... c_D
を求めることを考えます。測定データの y の値は x の値と係数の組 (c₀, c₁, c₂ .... c_D) を用いて (1) 式の様に表されます。

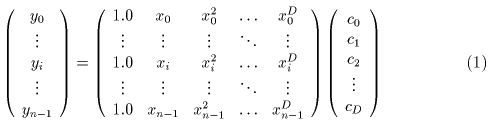
(1) 式を変形して (2) 式を得ます。

ここで、M_E を以下のように定義します。

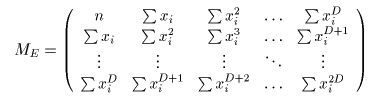
従って、係数の組は M_E の逆行列を計算することによって求めることが出来ます（ (3) 式）。

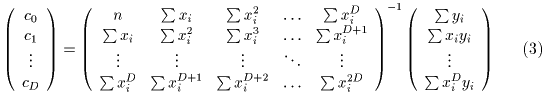
さて、プログラム上では逆行列をあらわに求めることはしないで、いわゆる掃き出し法で係数の組を求めます。この方が、逆行列を求めるより計算が速くなります。

2. 線形最小二乗法を行う Haskell プログラム lfit.hs

dat_file からデータを読み込み n 次のフィティングを行うときの処理の流れは以下の通りです。

0.0 が (3n+2) 個並んだリスト ls0 を用意する。
データを１行読み込む
読み込んだ行がコメント行なら次の行にスキップ
読み込んだ行から x, y の値を読み込み、リスト ls1 = [1.0, x, x² .. x²ⁿ, y, xy,...xⁿy] を作る。
ls0 =: zipWith (+) ls0 ls1
とし、値を加えていく。
dat_file を読み終わったら ls0 から組 M_E を作る。
note: dat_file を読み終えた時点で ls0 は ls_sum = [n, ∑x, ∑x²,..∑x²ⁿ, ∑y, ∑xy,..∑xⁿy] になる。
M_E を掃き出して係数の組を求める。
係数の組を表示する。

以下に線形最小二乗法を行う Haskell プログラムのコードを示します。

01:     ------------------------------------------------
02:     -- Linear least square fitting for X-Y data
03:     -- Usage: lfit [fitting order] [data file name]
04:     --
05:     -- data file format should be 'gnuplot' format
06:     --
07:     --                        by T.Shido
08:     --                        shido_takafumi@ybb.ne.jp
09:     --------------------------------------------------
10:     
11:     module Main where
12:     
13:     import IO
14:     import System
15:     
16:     -- reading and fitting data 
17:     fit :: Int -> String -> IO()
18:     fit n infname = bracket (openFile infname ReadMode)
19:                             hClose
20:                             (\h -> do hSetBuffering h LineBuffering
21:                                       ls_sum <- read_dat h (take (2+3*n) [0.0,0.0..])
22:                                       print $ map last $ sweep $ make_emat n ls_sum)
23:     --                      
24:      where read_dat h ls = do term <- hIsEOF h
25:                               if term
26:                                   then return ls
27:                                   else do line <- hGetLine h
28:                                           read_dat h (
29:                                                        if (head line) == '#' || line ==[]
30:                                                            then ls
31:                                                            else zipWith (+) ls (make_xy line))
32:     --
33:            make_xy str = take (2*n+1) lx ++ (map (*y) $ take (n+1) lx)
34:             where
35:                 xy = map read $ words str
36:                 x  = xy !! 0
37:                 y  = xy !! 1
38:                 lx = 1.0 : map (*x) lx   
39:     
40:     -- making an error matrix
41:     make_emat :: Int -> [Double] -> [[Double]]
42:     make_emat n dl = map make_line [0,1..n]
43:      where
44:          make_line i = (take (n+1) (drop i dl)) ++ [dl !! (i + 2*n + 1)]
45:     
46:     -- sweep a matrix
47:     sweep :: [[Double]] -> [[Double]]
48:     sweep mat = sweep' (length mat) 0 mat
49:     
50:     sweep' :: Int -> Int -> [[Double]] -> [[Double]]
51:     sweep' n i mat | i==n = mat
52:                    | otherwise = sweep' n (i+1) mat_next
53:      where a_i    = mat !! i
54:            a_ii   = a_i !! i
55:            v_c    = (take i [0.0,0.0..]) ++ (1.0 : map (/ a_ii)  (drop (i+1) a_i))
56:            mat_next = zipWith sweep_line [0,1..(n-1)] mat
57:            sweep_line  j ls | i==j      = v_c
58:                             | otherwise = take i ls ++
59:                                           (0.0 : (zipWith (\ x y ->  x - a_ki * y) 
60:                                                   (drop (i+1) ls) (drop (i+1) v_c)))
61:                                              where a_ki = ls !! i
62:                                               
63:     main :: IO ()
64:     main = do args  <- getArgs
65:               fit (read $ head args) (args !! 1)

行	説明
18	データファイルを読み込んで、最小二乗法を行う関数 fit を定義。引数はフィテッィングの次数 n とデータファイル名 infname
18	bracket を使って、ファイルの処理方法を詳しく記述する。 readFile を使って全部まとめて読み込んだ方が簡単だが、巨大なデータファイルにも対応できるよう一行ずつ読み込むようにする。
18	ReadMode でファイルを開く
20	IO バッファを LineBuffer にする。１行ずつ読み込むので、このサイズで十分。
21	read_dat を用いて ls_sum を求める。read_dat の定義は 24--30 行にある。 take (2+3n) [0.0,0.0..] で、0.0 が (2+3n) 個並んだリストが得られる。
22	ls_sum から組 M_E を作り (make_emat n)、掃き出して (sweep)、各行の最後の要素をとり、それを表示する。（プログラムはここでおしまい。） make_emat と sweep の定義はそれぞれ 41--44, 47--61 行にある。
24	read_dat の定義：ファイルハンドル (h) と Double のリスト (ls) を引数に取る。
24	hIsEOF h で、ファイルが終わっているか調べる。これは IO Bool なので、 Bool に変換するため <- を使う。
25	もし、ファイルが終わりなら、
26	ls を返す。
27	そうでなければ１行読み込んで、
28	read_dat h を繰り返す。
29	もし、読み込んだ行がコメントなら、
30	次の read_dat で ls をそのまま使う。
31	そうでなければ、読み込んだ行を make_xy (33--41 行）を使って、ls1 をつくり、 ls と ls1 のそれぞれの要素を足したものを次の read_dat で使う。(ここを参照) zipWith fun ls1 ls2 は map ( \ (e1, e2) -> fun e1 e2) $ zip ls1 ls2 と同じ。便利な記法で以下しばしば登場。
33	make_xy の定義。 take (2n+1) lx は [1.0, x, x^2.. x^(2n)] map (y) $ take (n+1) lx は [y, xy.... x^n * y]。
35	str を単語に分割してそれぞれを数に変換
36	その最初の要素が x
37	２番目の要素が y
38	lx は [1.0, x, x²,... ] 。ここを参照。
41	ls_sum から M_E を作る。適当に切り取ってつなぎかえるだけ。
47	掃き出し方を行う関数 sweep の定義
48	sweep は末尾再帰関数 sweep' を呼び出す。
50	sweep' の定義
51	終わったら（i==n なら）掃き出しが済んだ行列 mat を返す。
52	そうでなければ次の行に移って掃き出しを続ける。今回掃き出された行列を mat_next として次回の引数にする。
53	61 行目まで mat_next の求め方
53	まず、mat の i 行目を a_i とする。
54	mat の i 行目、i 列目の要素を a_ii とする。
54	a_i の各要素を a_ii で割ったものを v_c とする。掃き出しをしているので、(i-1) 番目の要素は 0.0 になっている。また、i 番目は定義より 1.0 になる。
55	mat_mext は mat の各行に sweep_line を作用させたもの。ちなみに (zip [0,1..(n-1)] mat) としているのは mat の行に行番号を振るため。
57	61 行目まで sweep_line の定義
57	i 行目は v_c を使う。
58	それ以外は (j, i) の要素が 0.0 になるようにする。つまり、 v_c の各要素に mat[j][i] の値を掛け、それを mat[j] の各要素から引く。 take i ls ++ (0.0 : map ... などとしているのは分かりきった値を再度計算しないため。
63	いよいよ main
64	コマンドラインの引数を取ってくる。
65	それに基づいて fit を実行する。

いかがでしょうか？
IO に随分手間がかかり、実際の処理は手短に書けていることが分かると思います。特に sweep は教科書に載っている定義そのままです。
データ処理部分は関数のパイプラインがくめるので（22 行目）、すっきりと書けます。この初歩的な例からも、Haskell は少ない IO と高度な処理をする課題に適しているといえます。

To do:
表示形式を見やすくする、係数の誤差を求めるなど改良したほうがよい点あります。興味のある人は試してください。（解答例はここにあります。）

3. コンパイルと実行

GHC を使って次のようにコンパイルします。

D:\doc\05-03\haskell>ghc -O lfit.hs -o lfit.exe

このようにすると一度 C 言語のソースコードを作成した後 gcc を使ってコンパイルされます。 --make を使ってコンパイルしたときより実行ファイルの形式が小さくなり、かつ速度が速くなることが期待されると云われています。

データファイル a.dat を 2 次でフィットするときは以下のようにします。
係数が 0 次から順に表示されます。

D:\doc\05-03\haskell>lfit 2 a.dat
[2.531727598665171,-0.5005644499197017,-2.9990377224373487e-2]

4. おまけ：テストデータを作る Haskell プログラム dat.hs

ついでにテストデータを作る Haskell プログラムも示します。乱数を使うとき参考にしてください。

01:     -----------------------------------------------------
02:     -- making test data for lfit.hs
03:     -- making a list of random numbers
04:     -- usage:
05:     --  dat [output_file_name] c0 c1 ... cn
06:     --
07:     -- by T.Shido (shido_takafumi@ybb.ne.jp)
08:     -----------------------------------------------------
09:     
10:     module Main where
11:     
12:     import Random
13:     import Time
14:     import System
15:     
16:     -- making a seed for randomR
17:     the_sec :: IO Int
18:     the_sec = do tm <- getClockTime
19:                  return $ sum $ zipWith (*)
20:                                   (map read $ split_str ':' ((words $ show tm) !! 3))
21:                                   [3600,60,1]
22:     
23:     -- split a string
24:     split_str :: Char -> String -> [String]
25:     split_str _ [] = []
26:     split_str c str = w : split_str c (case rest of{"" -> ""; _ -> tail rest})
27:      where (w, rest) = break (==c) str
28:     
29:     -- making a list of 'n' random numbers with in a range 'range'
30:     randR :: Int -> (Double, Double) -> IO [Double]
31:     randR n range = do seed <- the_sec
32:                        setStdGen (mkStdGen seed)
33:                        g <- getStdGen
34:                        return $ take n $ randomRs range g
35:     
36:     -- calculating y value at x
37:     calc_y lcoef x rd = foldl (+) rd  $ zipWith (*) lcoef lx
38:      where lx = 1.0 : map (*x) lx
39:     
40:     -- making a string like "y = randomR(-1.0 -- 1.0) + c0 + c1*x + c2*x**2 ...."
41:     sform lcoef = foldl (++) "y = randomR(-1.0 -- 1.0)"  $ zipWith sform' [0,1..] lcoef
42:      where sform' i c = let sc = " + " ++ show c
43:                         in case i of
44:                             0 -> sc
45:                             1 -> sc ++ " * x"
46:                             _ -> sc ++ " * x**" ++ (show i)
47:      
48:     main = do  av <- getArgs
49:                lrnd <- randR 100 (-1.0, 1.0)
50:                let coef = map read $ tail av
51:                writeFile (head av) $
52:                    foldl (++)
53:                          ("# A sample data for lfit.hs \n# made by dat.hs\n# " ++
54:                                       (sform coef) ++ "\n#\n")
55:                          (zipWith (\ x r -> (show x) ++ " " ++ (show $ calc_y coef x r) ++ "\n") 
56:                              [0,1..99] lrnd)

行	説明
17--21	今日の始まりからの秒数を数えます。
24--27	文字列 str を文字 c を区切りとして分割します。
30--34	range の範囲の Double の乱数 n 個からなるリストを返します。
37--38	係数の組 lcoef と x, 乱数 rd とから y の値を計算します。
41--46	"y = randomR(-1.0--1.0) + c0 + c1 x + c2 x2 ..... + cn xn" という文字列を返します。
48--56	av!!0 に、header と x = 0.0 -- 99.0 の x と y の値を出力します。

Haskell は純粋な関数型言語なので、そのつど乱数を作るより、あらかじめ乱数のリストを作って、そこから乱数を取り出すほうが便利でしょう。
Haskell で乱数を使う手順は以下の通りです。

時刻などの繰り返されない値に基づいて乱数の種を作る。
```
setStdGen (mkStdGen seed)
g <- getStdGen
```
ここで、seed は繰り返さない値。g は seed を基にした乱数の種です。

randoms または randomRs で乱数の無限リストを作る。

-- random Int, the range is the same as that of Int
random_Int = randoms g

-- random in a range, the range is defined by (lower_limit, upper_limit)
random_Range = randomRs (lower_limit, upper_limit) g

dat.hs とコンパイルと使用法は以下の通りです。

D:\doc\05-03\haskell>ghc -O dat.hs -o dat.exe

-- y = 2.5 + (-0.5)*x + (-0.03)*x**2 + random(-1.0 -- 1.0) を満たす x, y データを作り
-- それを a.dat に保存する。
D:\doc\05-03\haskell>dat a.dat 2.5 -0.5 -0.03

5. 終わりに

Haskell を使って実用的？なプログラムを書いてみました。ご参考になりましたら幸いです。

lfit.lzh は lfit.hs, dat.hs, a.dat を圧縮したものです。気が向いたらダウンロードして遊んでみてください。