12. 詰碁を解く Haskell プログラム

1. 初めに

この Haskell 講座の最初の文章で、Haskell は詰め将棋に向くと書いた手前、詰め物のプログラムを書いてみました。詰め将棋でも良かったのですが、将棋にはいろいろな種類の駒があり、プログラムが大きくなりそうなので、ルールが簡単な詰碁にしました。ここで示すやり方は詰め将棋にも使えるので、気が向いたら挑戦してみてください。

ここに示すプログラムは、コウやセキや長生にならない（つまり、二眼の生きの）黒先黒生の詰碁を解くことができます。二眼の黒先黒生に限定したのはこの条件ではプログラムが簡単に書け、実行時間も短くてすむからです。二眼の生きの場合は勝利条件が定義しやすいのですが、コウやセキや長生は勝利条件を定義するのは少し面倒です。また、黒先白死は、白石をとりきるまで読まなければならないので、手数が長くなり、従って、計算時間が長くなります。

このプログラムで用いた詰碁のルールを簡単に説明すると以下の様になります。

黒から打ち始め、黒は二眼の生きを目指す。
白は一番手数が長くなる手順を選ぶ。
二眼の生きとは相手が、任意の回数続けて打っても取られない石を指す。

詰碁のルールについてはひと目の詰碁―やさしい問題を反復練習などの囲碁の本を参照にしてください。 Web 上には適当なリソースが見当たりませんでした。ご存知の方はお知らせください。

ここで用いた問題はやさしい詰碁を解きましょうから拝借しました。

2. 遊び方

2.1. 動作環境

このプログラムは以下の環境で動作を確認しています。

WindowXP + Python2.4 + ghc6.4
Debian GNU Linux + Python2.3 + ghc6.4

2.2. コンパイル

tumego.lzh をダウンロードして解凍します。以下のファイルが生成します。

tumego.hs: Haskell ソースコード
tuemego.exe: Windows 用実行ファイル
goban.py: Python/Tk で書かれた GUI
q1_6.gbn, t2.gbn, q1_5.gbn, q2_2.gbn: 詰碁の問題

Linux の場合は、生成する tumego.hs を ghc 6.4 を使って次のようにコンパイルします。

>ghc -O3 tumego.hs -o tumego

"-O3" を使って最適化しないと遅くなります。一方、最適化したものは Lisp で書いて CMUCL でコンパイルしたものと同等の速度を示します。（CMUCL は Linux 上で動作する処理速度に定評のある Lisp 処理系です。）

2.3. 入力ファイルの作成

コマンドラインから

>python goban.py

と入力します。

升目を左クリックすると、空き地 → 黒石 → 白石 → 空き地と循環します。

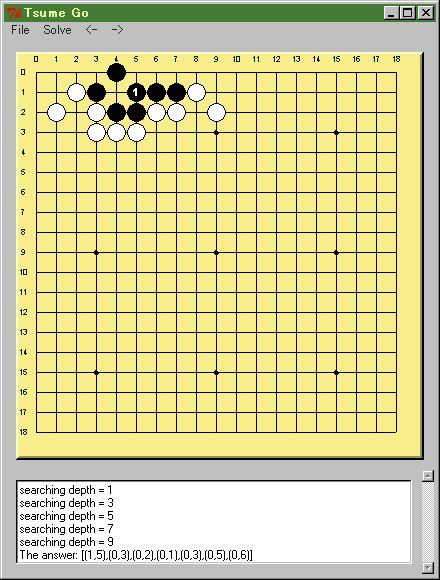
その後メニューバーの File → Save をクリックするとダイアログが開いてセーブするファイル名を聞いてきますので、名前をつけてセーブします。図１に例を示します。

図１: 石を置いた場面

2.4. 実行

以下の手順で実行します。

まず、メニューバーの File → Open で詰碁ファイルを開き、次にメニューバーの Solve をクリックします。
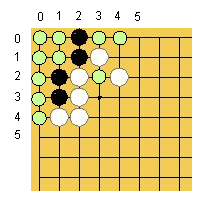
しばらく待っていると、碁盤の下の窓に答えが表示され、メニューの矢印がアクティブになるので、それをクリックすると石が置かれていきます。図２に例を示します。解が見つかるとメニューバーの矢印がアクティブになり、解を盤上に表示できます。

図２：詰碁を解いた場面

3. プログラムの方針

3.1. 碁盤の表現

碁盤をどのように表すかは、結構悩みます。碁盤に求められる条件は、

検索、挿入、更新のコストが小さい。
作成のコストが小さい。
ある碁盤に加えた変更が他の碁盤に影響を及ぼさない。

の３つです。この種の探索プログラムでは次々と碁盤を作っては破棄するので、作成のコストが小さいことが重要です。

碁盤なので Array データ型を使うのが自然に思えますが、このデータ型は検索のコストは小さいものの作成のコストが非常に大きいので不適当です。一方、連想リストは逆に検索のコストが大きく、あまり適当でありません。Array.IO, HashTable などの IO 型のデータは、碁盤を探索関数間で受け渡すのに適していません。

結局、すべてにおいてそこそこの速度を示す IntMap 型を採用しました。この型は key に Int をとる型で、通常の二分木より若干早くなっています。詳しくは GHC ドキュメントの Data.IntSet および、 Data.IntMap を見てください。

IntMap 型は key に Int しか取れないので、碁盤の座標を整数に変換したものを key とし、value は碁石の色 (Kuro, Shiro) にしました。石が無い升目はデータに加えません。こうすることによって、詰碁のように広い盤面に石があまり無い場合も、効率よく表せることができます。

3.2. 探索方針

詰碁のような詰め物のプログラムでは、黒番は、白番がどのように対応しても勝利条件が達成できる手を選ばなければなりません。Haskell の Maybe 型の Monad を使うとこのようなプログラムが簡単に書けます。黒番の時は、条件を満たす手が１つでもあればいいので、msum をつかって表すことができます。 msum は最初に見つかった Just a を返す関数です。

一方、白番のときは白がどう打っても黒の勝利条件が達成されなければならないので、すべての値が Just a のときだけ、Just [a] を返す関数 mapM を使います。

msum と mapM は次のように使います。

01:     --- msum and mapM
02:     
03:     import Monad
04:     
05:     msqrt :: Double -> Maybe Double
06:     msqrt x | x >= 0 = Just (sqrt x)
07:             | otherwise = Nothing
08:     
09:     ls0 = [ 1.0, -1.0, 2.0, 3.0]
10:     ls1 = [ 1.0, 2.0, 3.0]
11:     
12:     msum0 = msum $ map msqrt ls0
13:     mapM0 = mapM msqrt ls0
14:     mapM1 = mapM msqrt ls1

Main> msum0
Just 1.0
Main> mapM0
Nothing
Main> mapM1
Just [1.0,1.4142135623731,1.73205080756888]

つまり、黒番のときは msum を使って、勝利条件に達する手順をひとつ返し、白番の時は、mapM を使ってすべての応手にたいして黒番の勝利条件に達するとき、手順のリストを返えすようにして深さ優先探索をすればいいことになります。

tumego.hs では関数 searching を使って深さ優先探索を行います。 searching の引数は、最大の読みの深さ (nmax)、現在の読みの深さ (nnow)、碁盤を表す IntMap (g)、守備側の石の色 (cdef)、現在打つ石の色 (cnow)、これまでの手順 (path)、直前の手 (pp)、手の選択肢 (choices) です。 searching は次のような動作をします。

黒が生きているときは、この局面に至るまでの手順を返す。
読みの最大深さに達したときは fail
碁盤に黒石が無いときは fail
選択肢が無いときは、黒の手番なら fail 白の手番なら手順を返す。
黒番のときは msum を使って、最初に見つかった手順を返す。
白番の時は mapM と return_longest を使って、すべての選択肢に対して手順が帰ってきたら、そのうちの最長手順を返す。

01:     --- solving tumego using depth first search
02:     searching :: Int -> Int -> GBN -> Iro -> Iro -> [Int] -> Int -> [Int] -> Maybe [Int]
03:     searching nmax nnow g cdef cnow path pp choices 
04:         | is_iki g cdef = return (reverse path)
05:         | nnow == nmax = fail "reached to the limit"
06:         | not (s_exist g cdef) = fail "all stones are captured"
07:         | choices1==[] = if (cdef == cnow) then fail "no way" else return (reverse path)
08:         | cdef == cnow = msum $ map searching_next choices1
09:         | otherwise = return_longest $ mapM searching_next choices1
10:      where
11:          captured = if (nnow > 0) then cap_stones g cnow pp else []
12:          g1 = sweep_gbn g captured
13:          choi = choices ++ captured
14:          choices0 = if (nnow > 0)
15:                         then
16:                              if (cnow == cdef) then choi else union choi (surround g1 pp)
17:                         else choices
18:          choices1 = gordering g1 cdef cnow $ filter (\x -> is_safe g1 cnow x) choices0
19:          searching_next p0 = searching nmax (nnow+1) (g_add g1 p0 cnow)
20:                                 cdef (opposite cnow) (p0:path) p0 (delete p0 choices0)
21:          return_longest Nothing = fail "no chance"
22:          return_longest (Just ls) = return (find_longest ls)
23:

このプログラムでは最大の読みの深さ (nmax)を 1 からはじめ、解が見つかったらそれを返して停止し、見つからなければ nmax を２つ増やして探索を続けます。この手法（反復深化法）は計算時間がかかりますが、プログラミングが簡単で、メモリーの消費も少ないという利点があります。また、msum, mapM が使えるという利点があります。

3.3. 手の選択肢を求める

碁盤は広いので、空いている点全てについて読むというのは現実的でありません。詰碁の場合は、着手は生きようとしている石（この場合は黒石）付近に限定されます。

選択肢は次の基準で選びます。

盤上にある黒石に隣接している点。
盤上にある黒石の斜めの点。
盤上にある黒石から１つ飛んだ点。ただし間が空いている場合に限る。

具体例を示すと、下図の緑丸の位置が選択肢です。また、手順が進んで、新たな黒石が盤上に置かれるとその石の周りも選択肢に加えます。

3.4. 手の選択肢の優先順位を決める

着手にスコアをつけ、スコアの高い手から探索することで、無駄な手を読む手間が省け、探索時間を短くすることができます。

碁は打った石が動けないゲームなので、黒番、白番とも急所は同じ場所になります。（いわゆる”敵の打ちたいところへ打て”ということです）選択肢にある手を次の規則でスコアをつけ、スコアの大きい手から探索します。

黒が完全に生きる場所はスコア 3
黒に二眼ができる場所はスコア 2
白番で、黒のダメを詰める場所はスコア 1
その他はスコア 0

4. コードの概説

次の表に各関数の説明を示します。

行	関数名	説明
43	opposite c	c が Kuro なら Shiro, Shiro なら Kuro を返す。
50	find_longest ls	ls の要素で、最長のリストを返します。
64	p2int p	碁盤の座標 p を整数に変換します。
69	int2p i	整数 i を碁盤の座標に変換します。
81	g_add g p c	碁盤 g の位置 p に色 c の石を置きます。
87	g_del g p	碁盤 g の位置 p から石を取り除きます。
93	g_empty g p	碁盤 g の位置 p に石がないか調べます。なければ True
99	p2c g p	碁盤 g の位置 p の石の色を調べます。
105	find_next p	位置 p に隣接する座標を返します。
115	s_exist g c	碁盤 g に色 c の石があるか調べます。あれば True
122	is_safe g c p	碁盤 g の位置 p に色 c の石が置けるか調べます。
128	is_safe0 g c p	碁盤 g の位置 p に色 c の石を置いたとき呼吸点があるか調べます。
146	is_csr	碁盤 g の位置 p に色 c の石を置いたとき相手の石を取れるかどうか調べます。
168	find_ga g c p	碁盤 g の位置 p にある色 c の石と連続した石と、その呼吸点のリストのタプルを返します。
186	cap_stones g c p	碁盤 g の位置 p にある色 c の石とそれに連なる石で、取られる石を返します。
208	up_gbn g c p	碁盤 g の位置 p に色 c の石を置いて碁盤を更新します。
216	sweep_gbn g ps	碁盤 g から ps にある石を取り除きます。
223	is_iki g c	碁盤 g で色 c の石が生きているか調べます。生きていれば True
230	all_akidame g c	碁盤 g で色 c の石の全ての呼吸点を返します。
259	is_nigan g c	碁盤 g で色 c の石が二眼（欠け目も含む）か調べます。二眼ならば True
277	ini_op g ls c	問題図 g の選択肢を作成します。
290	surround g p	碁盤 g の位置 p の "周り" の位置のリストを返します。
304	gordering g cdef cnow ps	スコアに基づいて選択肢を sort します。
313	gweighting g cdef cnow p	選択肢にスコアをつけます。
324	gsorting	スコアを Ordering に変換します。
333	searching	深さ優先探索を行います。
359	kuroiki	反復深化法を行います
386	init_goban	石の位置のリストから碁盤を初期化します。
394	do_tsumego str	str から石の位置のリストを作り kuroiki に渡します。
405	rm_cmt str	str からコメントを取り除きます。
415	main	main 関数です。引数で指定されたファイルを読み、その内容を do_tsumego に渡します。

5. 終わりに

5.1. Haskell は探索型ゲームプログラムに適しているか？

プログラムはかなり余白を持たせて書いたので、 400 行ほどになりました。かなりの部分が、打てる場所の判定と、二眼の生きの判定に関する部分に費やされました。一方、探索プログラム自体は少ない行数で実現できています。

これと同様のプログラムを Lisp で書いても 400 行ほどになります。 Haskell 版は Lisp に比べて、特に短くなるというわけではなく、実行速度もほとんど変わりませんが、以下の点で Lisp に比べて若干優れていると思われます。

Common Lisp では空リストと失敗に両方 nil を使うが、この種の探索プログラムではバグの原因になる。実際、tumego.hs の Lisp 版を書いたときこれがバグのもとになり、気づくまでしばらくかかった。探索に失敗したら明示的に 'fail を返すようにして解決。
探索プログラムを書く上で便利な msum, mapM などの関数が備わっている。 Lisp では自分で書く必要がある。
IntMap などの便利なデータ型が使える。Lisp では連想リストを使わざる得なかった。 IntMap 抜きでは碁盤を表現するのにかなり複雑なことになるだろう。

感じとしては、Haskell はこの手のプログラムを書くために開発されたのではないかと思えるほど書きやすかったです。遅延評価のおかげで、評価しなくていい枝は評価されないので、プログラムの構造をすっきり書けます。 Lisp を含むほかの言語では同等のことを行うために (Lisp の) return, catch -- throw などのジャンプ命令を使う必要があります。
Haskell を用いた探索的プログラミングについてはなぜ関数プログラミングは重要かを見てください。

5.2. やること

ここで示したプログラムは詰碁プログラムとしては初歩的なものですが、これを基に改良を加えていけば完成度が高いものになると思います。

セキに対応する：着手にパスを含めることによって可能になります。Haskell なら比較的簡単かも。
コウに対応する：これは少し難しいかも？特に両コウにどう対処するかは問題。
着手のスコアをもっときめ細かくつける：例えば、３方が黒に囲まれた点などにも点数をスコアがきめ細かくなります。
バグ抜き
高速化: 現状では遅すぎる。

5.3. バグ

すでに黒が生きているのに白が無駄な手を打つことがある。（表示する手順では無駄手を除いている）