1. Sather vs C++: a performance comparison

1. Is Sather really faster than C++?

According to Wikipedia, Sather code often performs better than the corresponding C++ code. To see it is true, I wrote a simple time consuming program which uses features of Sather and C++. The program is to enumerate the number of primes. Found primes are stored in a list.

2. C++ version

[code 1] shows the C++ version. Found primes are stored in vector<int>. (It just uses the vector class but not uses many other C++ features. I am thinking better example..... It should be OK for now!)

01:     // g++ -O2 nprime.cpp -o nprime_cpp
02:     #include <iostream>
03:     #include <vector>        
04:     
05:     #define W 500
06:     
07:     using namespace std;
08:     
09:     
10:     inline bool primep(vector<int>& plist, int i){             
11:       for( vector<int>::iterator iter = plist.begin();iter != plist.end(); iter++){
12:         int j = *iter;
13:         if(j*j>i) return true;
14:         if(i%j==0) return false;
15:       }
16:     }
17:     
18:     void nprime(int m){
19:       vector<int> plist;
20:       plist.push_back(2);
21:       plist.push_back(3);
22:       for(int j =5, r=3; j <= m; j+=2, r++){
23:         if(primep(plist, j)) plist.push_back(j);
24:         if(r==W){
25:           cout << j << " " << plist.size() << "\n";
26:           r = 0;
27:         }
28:       }
29:     }
30:     
31:     int main(int ac, char** av){
32:       if(ac ==2){
33:         int m = atoi(av[1]);
34:         if(m > 10000){
35:           cout << "#Limit, N of primes\n0 0\n";
36:           nprime(m);
37:           return 0;
38:         }else{
39:           cerr << "limit should be > 10000\n";
40:         }
41:       }else{
42:         cerr << "Usage: nprime_cpp N\n";
43:       }
44:     }

Note

inline bool primep(vector<int>& plist, int i):
It returns true if i is prime. It is a inline function for speed up. It checks if i is divisible by primes already found.
void nprime(int m):
It adds a new prime to plist. It output the number of primes every thousand to the standerd output.
int main(int ac, char** av):
It checks the arguments and call nprime if OK.

The program output the number of primes from 0 to N (av[1]) every 1000. I compiled the program using g++ and counted the number of primes up to 10000000.

$ g++ -O2 nprime.cpp -o nprime_cpp

$ time ./nprime_cpp 10000000 > nprime_cpp.dat

real    0m8.365s
user    0m8.245s
sys     0m0.004s

It takes only 8.365 second. Pretty fast.

3. Sather version

[code 2] shows the Sather version of the same program. It uses iterator for looping. I feel elt! and step! are more speedy than while!.

01:     -- primitive counting prime numbers program
02:     -- sacomp -O_fast nprime.sa -o nprime_sa
03:     
04:     class MAIN is
05:        attr plist :LIST{INT}; 
06:        const w:INT := 500;
07:     
08:        private primep(i:INT):BOOL is
09:           j:INT;
10:           
11:           loop 
12:     	 j :=self.plist.elt!;
13:     	 if j * j > i then
14:     	    return true;
15:     	 end;
16:     	 if i % j = 0 then
17:     	    return false;
18:     	 end;
19:           end;
20:        end;
21:     
22:     
23:        nprime(maxi:INT) is
24:           j,r:INT;
25:           self.plist := #(|2,3|);
26:           r := 3;
27:           loop
28:     	 j := 5.step!((maxi-3)/2, 2);
29:     	 if self.primep(j) then
30:     	    self.plist.append(j);
31:     	 end;
32:     	 if r = w then
33:     	    #OUT + j + " " + self.plist.size + "\n";
34:     	    r := 0;
35:     	 end;
36:     	 r := r+1;
37:           end;
38:        end;
39:        
40:        main(av:ARRAY{STR}) is
41:           if av.size = 2 then
42:     	 m:INT := av[1].cursor.get_int;
43:     	 if m <= 10000 then
44:     	    #ERR + "limit should be > 10000\n";
45:     	 else
46:     	    #OUT +"# limit, N of primes\n0 0\n";
47:     	    nprime(m);
48:     	 end;
49:           else
50:     	 #ERR + "Usage: nprime N\n"
51:           end;
52:        end;
53:     end;

The algorithm is completely the same as that of the C++ version.

$sacomp -O_fast nprime.sa -o nprime_sa
$time nprime_sa 10000000 > nrpime_sa.dat

real    0m14.262s
user    0m11.617s
sys     0m0.016s

It takes 14.262 second. It is also pretty fast but slightly slower than the C++ version. I may be just because the program is not large enough. Nevertheless, it is much faster than those written in Python and Scheme, indicating that Sather is an attractive language with easy writing and fast speed. If you need more speed you can combine Sather and C or Fortran easily.

Fig. 1. Number of primes.

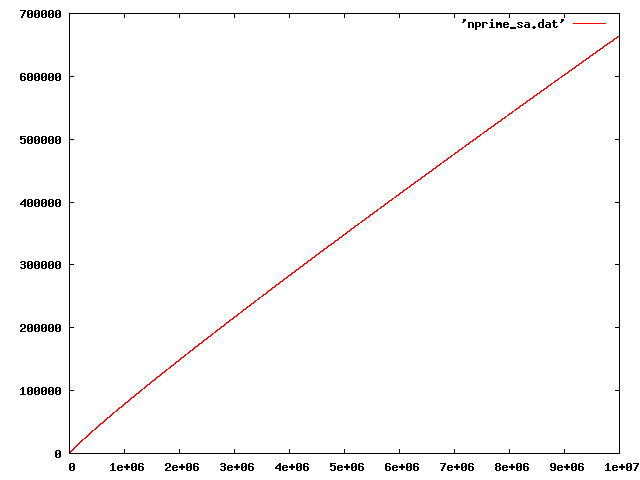
Figure 1 shows Number of primes as a function of number, which shows that density of primes decreases as number increases gradually.

4. Try Sather!

The result encouraged me to learn Sather. Sather is suitable for large scale and speed required programs. Even the C++ version is faster in this case, C++ is somehow tricky and tiny mistakes make it slow easily. I use Python or Scheme if I do not need speed. But I will use Sather when I need it.

The readability of Sather is much better than those of C and C++, which is apparent in large scale programs.

I am wondering why Sather is so minor?