17. Lazy evaluation

1. Introduction

Lazy evaluation is a way of computing in which values are not calculated until they are required. The lazy evaluation includes iteration in data structure naturally and represents infinity in a simple matter, which promote modularity of programs. See Why Functional Programming Matters on the benefit of the lazy evaluation.

Haskell is well recognized as a programming language that totally adopts lazy evaluation. Scheme also adopts it (even the adoption is partially).

2. Functions for the lazy evaluation

Following functions are defined in the R⁵RS, which deal with lazy evaluation. Intermediate states are called promise in that the way of evaluation is defined and the evaluation is not done yet. The final values are calculated by applying force to the promises.

(delay proc): making a promise from the proc.
(promise? obj): returning #t if obj is a promise.
(force promise): Calculating a value from the promise.

3. A simple example of the lazy evaluation

[sample 1] shows a simple example of the lazy evaluation. In this sample, a promise is produced by applying the function delay to (+ 1 2), then evaluate the promise by the function force.
[sample 1]

(define laz (delay (+ 1 2)))
;Value: laz

laz
;Value 11: #[promise 11]

(promise? laz)
;Value: #t

(force laz)
;Value: 3

(* 10 (force laz))
;Value: 30

Notice that promises are not consumed by force, which means that the function force has no side effect. As a consequence, you can reuse promises.

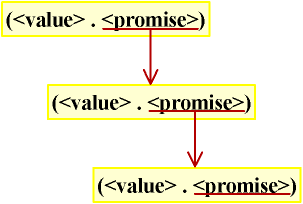
4. Representation of infinite sequences using the lazy evaluation

Now let's make infinite sequences using the lazy evaluation. First I will define some basic functions to treat infinite sequences. Then I will make infinite sequences using these functions and apply infinite sequences to numerical calculations.

A infinity sequence is represented by 'a nested structure' of a cons cell shown in eq. (1), whose car and cdr parts are a final value and a promise, respectively. Another cons cell with a structure of eq. (1) is produced by forcing the cdr part, and you can repeat this procedure up to infinity as shown in fig. 1. Even the nested structure of cons cells is similar to that of ordinary lists, using promises as the cdr part makes it possible to represent infinite sequences.

(<val> . <promise>)    (1)

Figure 1. A implementation of a infinity sequence using a cons cell whose car and cdr parts are a final value and a promise, respectively.

4.1. Basic functions and a macro for infinite sequences

[code 1] shows basic functions and a macro for infinite sequences. The most important one among them is lazy-map, which is used for operations of infinite sequences.

As lazy-cons contains a special form delay which delays evaluation, it should be defined as a macro.

[code 1]

01:     ;;;;; basic functions and a macro
02:     
03:     ;;; car for lazy evaluation
04:     (define lazy-car car)
05:     
06:     ;;; cdr for lazy evaluation
07:     (define (lazy-cdr ls)
08:       (force (cdr ls)))
09:     
10:     ;;; lazy cons
11:     (define-syntax lazy-cons
12:        (syntax-rules ()
13:           ((_ a b) (cons a (delay b)))))
14:     
15:     ;;; lazy map
16:     (define (lazy-map fn . lss)
17:       (if (memq '() lss)
18:           '()
19:         (lazy-cons (apply fn (map lazy-car lss))
20:                    (apply lazy-map fn (map lazy-cdr lss)))))
21:     
22:     ;;; lazy filter
23:     (define (lazy-filter pred ls)
24:       (if (null? ls)
25:           '()
26:         (let ((obj (lazy-car ls)))
27:           (if (pred obj)
28:               (lazy-cons obj  (lazy-filter pred (lazy-cdr ls)))
29:             (lazy-filter pred (lazy-cdr ls))))))
30:     
31:     ;;; returns n-th item of the lazy list
32:     (define (lazy-ref ls n)
33:       (if (= n 0)
34:           (lazy-car ls)
35:         (lazy-ref (lazy-cdr ls) (- n 1))))
36:     
37:     ;;; returns first n items of the ls
38:     (define (head ls n)
39:       (if (= n 0)
40:           '()
41:          (cons (lazy-car ls) (head (lazy-cdr ls) (- n 1)))))

(lazy-car ls): It is same as (car ls) because the car part is a final value.
(lazy-cdr ls): It calculates the 'final' value of the cdr part (promise) of the ls.
(lazy-cons a b): It is a macro expanded to (cons a (delay b)). If the operation is defined as a function, the b is evaluated immediately and delay does not have any sense in this case.
(lazy-map fn . lss): It is a map function for the lazy evaluation, which is the most important in the [code 1]. Notice that it returns a cons cell consisting of a final value (car part) and a promise (cdr part).
(lazy-filter pred ls): It is a filter function for the lazy evaluation. It filters the ls and returns a 'infinite sequence' consisting of items that satisfy the pred.
(lazy-ref ls n): It returns the n-th item of ls, a 'infinite sequence'.
(head ls n): It returns first n items of the ls (lazy evaluated list).

4.2. Infinite sequences

Infinite sequences are represented concisely using lazy-cons and lazy-map. I present two examples:

Sequences in which the next term is defined by the previous term such as arithmetic and geometric sequences.
Fibonacci series.

4.2.1. Sequences in that the next term is defined by the previous term

Sequences in that the next term is defined as a function (f) of the previous term:
a_i+1 = f(a_i)
can be represented by (inf-seq a0 f) in [code 2], where a0 and f are the initial term and the function to calculate the subsequent term.

(inf-seq a0 f) is defined recursively and the definition shows clearly that the initial term is a0, that the second term is (f a0), and that (n+1)-th term is represented by (f a_n).

Arithmetic and geometric sequences are defined by (ari a0 d) and (geo a0 r), respectively, where a0, d and r are the initial term, common difference, and geometric ratio, respectively. These functions are defined using the function inf-seq. [code 2]

01:     ;;;;  sequences
02:     
03:     ;;; infinite sequences represented by a_(n+1) = f(a_n)
04:     (define (inf-seq a0 f)
05:       (lazy-cons a0 (inf-seq (f a0) f)))
06:     
07:     ;;; arithmetic sequence
08:     (define (ari a0 d)
09:       (inf-seq a0 (lambda (x) (+ x d))))
10:     
11:     ;;; geometric sequence
12:     (define (geo a0 r)
13:       (inf-seq a0 (lambda (x) (* x r))))

Let's check if infinite sequences are produced by inf-seq (sample 2). Make two geometric sequences:

g1, initial term 1, ratio 2.
g2, initial term 1, ratio 1/2.

then evaluate the first 10 terms using the head. You will see that the two geometric sequences are produced properly.
Next, calculate products of terms in g1 and g2 using the lazy-map and evaluated the first 10 terms using the head. You will see a sequence of 1, which indicates that the calculation is done properly.

Now, let's play with arithmetic sequences and the lazy-filter. First, make an arithmetic sequence ar1 by (ari 1 1). The result of (head ar1 10) shows that an arithmetic sequence (1 2 3 ....) is produced by (ari 1 1). Then extract even numbers from the ar1 using the lazy-filter and evaluate first 10 terms using the head. You will see (2 4 6 8 10 12 14 16 18 20), which indicate that the lazy-filter works properly.

[sample 2]

(define g1 (geo 1 2))
;Value: g1

(define g2 (geo 1 (/ 1 2)))
;Value: g2

(head g1 10)
;Value 12: (1 2 4 8 16 32 64 128 256 512)

(head g2 10)
;Value 13: (1 1/2 1/4 1/8 1/16 1/32 1/64 1/128 1/256 1/512)

(head (lazy-map * g1 g2) 10)
;Value 14: (1 1 1 1 1 1 1 1 1 1)

(define ar1 (ari 1 1))
;;Value: ar1

(head ar1 10)
;;Value 15: (1 2 3 4 5 6 7 8 9 10)

(head (lazy-filter even? ar1) 10)
;;Value 16: (2 4 6 8 10 12 14 16 18 20)

4.2.2 Fibonacci series

Fibonacci series is defined like as follows:

fib(1) = 1
fib(2) = 1
fib(n+1) = fib(n) + fib(n-1)

Code 3 shows a Scheme implementation of the Fibonacci series using lazy-cons and lazy-map. As shown in this code, the definition on Scheme is quite similar to that of mathematical one. In addition, terms are calculated in the order of O(n).
Values in [sample 3] are calculated immediately.

[code 3]

01:     (define fib
02:       (lazy-cons 1
03:                  (lazy-cons 1
04:                             (lazy-map + fib (lazy-cdr fib)))))

[sample 3]

(head fib 20)
;Value 12: (1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765)

(lazy-ref fib 100)
;Value: 573147844013817084101

4.3. Application of the lazy evaluation to numerical calculations

Followings are Scheme version of the code in Why Functional Programming Matters. See also SICP 3.5. Streams on the application of the lazy evaluation to numerical calculations.

4.3.1. Newton–Raphson square roots

Newton–Raphson method is to calculate the square root of N by using initial value a0 and eq. (2).

     a(n+1) =  (a(n) + N/a(n)) / 2                   (2)

If eq (2) converges to a ultimate value a,

      a =  (a +  N/a) / 2
⇒
      2a = a +  N/a
      a =  N/a
      a*a = N
      a =  √N

, which indicates that the ultimate value a is the square root of N. As the next term of the sequence is a function of the previous term (as shown in eq. (2)), The sequence is represented by using inf-seq.
Code 4 shows a program to calculate square roots. In code 4, the initial value is fixed at 1, which should be OK because the sequence converges quickly.

[code 4]

01:     ;;; Newton-Raphson method
02:     (define (newton-raphson n)
03:       (inf-seq 1 (lambda (x) (/ (+ x (/ n x)) 2))))
04:     
05:     ;;; returning a reasonable answer.
06:     ;;; If the ratio of successive terms is in (1 - eps) and (1 + eps),
07:     ;;; or the following term is zero,
08:     ;;; the function returns it.
09:     (define (lazylist->answer ls eps)
10:       (let ((e1 (- 1.0 eps))
11:             (e2 (+ 1.0 eps)))
12:         (let loop ((val (lazy-car ls))
13:                    (ls1 (lazy-cdr ls)))
14:           (let ((val2 (lazy-car ls1)))
15:             (if  (or (zero? val2) (< e1 (/ val val2) e2))
16:                 (exact->inexact val2)
17:               (loop val2 (lazy-cdr ls1)))))))
18:     
19:     ;;;
20:     (define (my-sqrt n eps)
21:       (lazylist->answer (newton-raphson n) eps))

(newton-raphson n): It is a function to make a lazy list of approximated values of the square root of n.
(lazylist->answer ls eps): It checks if the convergence is good enough. if so it returns the answer of the numerical calculation.
The function returns the second term of successive terms of ls (say t₁ and t₂) if (1 - eps) < t₂/t₁ < (1 + eps) or t₂ = 0.
(my-sqrt n eps): It calculates the square root of n in a relative error of eps.

(my-sqrt 9 0.0000001)
;Value: 3.

4.3.2. Numerical differentiation

The easydiff in [code 5] is a simple way of numerical differentiation, where f, x, and h are function to be differentiated, the x value, and Δx, respectively. Theoretically, approximation is getting better if h is reaching to zero. In practise, however, because the precision of numerical values in computers is limited, too small value of h causes errors.

To solve this problem, we make an lazy list of h as shown in lazylist-diff. The lazy list is a geometric sequence with a initial value of h0, and ratio of 0.5. Then we make a lazy list of approximated values of differentiation corresponding to the lazy list of h.

It could be better to accelerate the convergence even the answer can be obtained by:

(lazylist->answer (lazylist-diff h0 f x) eps)

A function super is the convergence accelerating function. See Why Functional Programming Matters about the accelerating technique. The accelerating technique is substantially complicated if you use a conventional programming language. On the contrary, it can be implemented in a simple way using the lazy evaluation. In addition, because of the high modularity, you can reuse the code for other issues such as numerical integration (section 4.3.3). Code 6 reuses the acceleration functions defined in code 5.

[code 5]

01:     ;;; differentiation
02:     
03:     ;;; primitive function for differentiation
04:     (define (easydiff f x h)
05:       (/ (- (f (+ x h)) (f x)) h))
06:     
07:     ;;; create a lazy list of approximation for differentiation
08:     (define (lazylist-diff h0 f x)
09:       (lazy-map (lambda (h) (easydiff f x h)) (geo h0 0.5)))
10:     
11:     ;;; eliminate error from the approximation
12:     (define (elimerror n ls)
13:       (let ((a (lazy-car ls))
14:             (b (lazy-second ls))
15:             (c (fix:lsh 1 n)))   ; (expt 2 n)
16:         (lazy-cons
17:          (/ (- (* b c) a) (- c 1))
18:          (elimerror n (lazy-cdr ls)))))
19:     
20:     ;;; estimate `n' in elimerror
21:     (define (order ls)
22:       (let* ((a (lazy-car ls))
23:              (b (lazy-second ls))
24:              (c (lazy-ref ls 2))
25:              (d (- (/ (- a c) (- b c)) 1.0)))
26:         (cond
27:          ((< d 2) 1)
28:          ((<= 2 d 16) (inexact->exact (round (log2 d))))
29:          (else 4))))
30:     
31:     ;;;
32:     (define (log2 x)
33:       (/ (log x) (log 2)))
34:     
35:     ;;; improve convergence of the lazy list of the approximation
36:     (define (improve ls)
37:       (elimerror (order ls) ls))
38:     
39:     ;;; return the second value of the lazy list
40:     (define (lazy-second ls)
41:       (lazy-car (lazy-cdr ls)))
42:     
43:     ;;; further improve the convergence of the list
44:     (define (super ls)
45:       (lazy-map lazy-second (inf-seq ls improve)))
46:                 
47:     
48:     ;;; calculate the differentiation of function `f' at x within error eps
49:     ;;; h0 is initial window width
50:     (define (diff f x h0 eps)
51:       (lazylist->answer (super (lazylist-diff h0 f x)) eps))

(diff sin 0.0 0.1 0.0000001)
;Value: .9999999999999516

(diff exp 0.0 0.1 0.000001)
;Value: .9999999991733471

4.3.3. Numerical integration

The convergence acceleration functions can be reused for numerical integration without any modification. As a starting point, we make a rough approximation using easyintegrate. The function lazylist-integrate uses a lazy list to improve the approximation by splitting the range at the middle point to apply easyintegrate recursively. The function can be defined in a simple way using the lazy-map. Finally, the convergence is accelerated and returns the converged value by the function integrate.

[code 6]

01:     ;;; integration
02:     
03:     ;;; primitive integration
04:     (define (easyintegrate f a b)
05:       (* (/ (+ (f a) (f b)) 2) (- b a)))
06:     
07:     ;;; create the lazy list of approximation for integration
08:     (define (lazylist-integrate f a b)
09:       (let ((mid (/ (+ a b) 2)))
10:         (lazy-cons (easyintegrate f a b)
11:                    (lazy-map + (lazylist-integrate f a mid)
12:                                (lazylist-integrate f mid b)))))
13:     
14:     ;;; integrate function `f' in a range of `a' and `b' within error `eps'
15:     (define (integrate f a b eps)
16:       (lazylist->answer (super (lazylist-integrate f a b)) eps))

(define pi (* 4 (atan 1)))
;Value: pi

(integrate sin 0 pi 0.0000001)
;Value: 2.000000002272428

(integrate exp 0 1 0.0000001)
;Value: 1.7182818277724858

(- (exp 1) 1)
;Value: 1.718281828459045

5. Summary

Lazy evaluation allows us to include reputation into data structure concisely. This feature promotes the modularity of programs and makes the code tight.

Check web sites on Haskell to know more about the lazy evaluation.

You can download the codes shown in this page from here.