HOME Yet Another Scheme Tutorial download Post Messages

8. Higher Order Functions

1. Introduction

Higher order functions are functions that takes functions as arguments. They are used for mapping, filtering, folding, and sorting of lists.

The higher order functions promote modularity of programs. Writing higher order functions that are applicable in many cases makes program readable rather than writing recursive functions for individual cases.

For instance, using a higher order function for sort allows sorting by variety of conditions, which separates the sorting condition and the sorting procedure sharply. The function sort takes two arguments, one is a list to be sorted and the other is an ordering function. The following shows the sort of a list of integral numbers in ascending order by their size. The function < is the ordering function of two numbers. 

(sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) <)
⇒ (2239 2644 2828 2958 4179 5340 6729 7754 7883 9099)
On the other hand, sort by the size of last two digits can be done like as follows: 
(sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) 
      (lambda (x y) (< (modulo x 100) (modulo y 100))))
⇒ (2828 6729 2239 5340 2644 7754 2958 4179 7883 9099)
As shown here, sorting procedures such as quick sort, merge sort, etc. and ordering functions are separated completely, which promote reuse of codes.

In this chapter, I will explain about pre-defined higher order functions and then about how to make your own. As Scheme does not distinguish procedures and other data structures, you can make your own higher order functions quite easily by just giving procedures as arguments.

Actually, substantial parts of pre-defined functions in Scheme is higher order functions, because Scheme does not have a syntax that defines block structure, and because lambda expression is used as a block.

2. Mapping

Mapping is a procedure that treats all list items in a same manner. Two mapping functions are defined in the R5RS: One is map which returns the converted list and the other is for-each which is used for side effects.

2.1. map

The format is like as follows: 
(map procedure list1 list2 ...)
The procedure is a symbol bound to a procedure or a lambda expression. Number of lists as arguments depend on the number of arguments of the procedure.

Example: 

; Adding each item of '(1 2 3) and '(4 5 6).
(map + '(1 2 3) '(4 5 6))
⇒ (5 7 9)

; Squaring each item of '(1 2 3)
(map (lambda (x) (* x x)) '(1 2 3))
⇒ (1 4 9)

2.2. for-each

The format is the same as that of map. The function does not return a specified value and is used for side effects.

Example: 

(define sum 0)
(for-each (lambda (x) (set! sum (+ sum x))) '(1 2 3 4))
sum
⇒ 10

Exercise 1

Write followings using map.
  1. A function that makes it twice that each item of a list of numbers.
  2. A function that subtracts items of two lists.

3. Filtering

Even filtering functions are not defined in the R5RS, keep-matching-items and delete-matching-items are available in the MIT-Scheme. Other implementations should have similar functions. 
(keep-matching-items '(1 2 -3 -4 5) positive?)
⇒ (1 2 5)

Exercise 2

Write followings:
  1. filtering out even numbers in a list.
  2. filtering out numbers (x) that are not 10 ≤ x ≤ 100.

4. Folding

Even folding functions are not defined in the R5RS, functions reduce etc. are available in the MIT-Scheme. 
(reduce + 0 '(1 2 3 4))                 ⇒  10
(reduce + 0 '(1 2))                     ⇒  3
(reduce + 0 '(1))                       ⇒  1
(reduce + 0 '())                        ⇒  0
(reduce + 0 '(foo))                     ⇒  foo
(reduce list '() '(1 2 3 4))            ⇒  (((1 2) 3) 4)

Exercise 3

  1. Write a function that squares each item of a list, then sums them and then makes square root of it.

5. Sorting

Even sorting functions are not defined in the R5RS, functions sort (merge-sort) and quick-sort are available in the MIT-Scheme. 
(sort '(3 5 1 4 -1) <)
⇒ (-1 1 3 4 5)

Exercise 4

Write followings:
  1. Sort by magnitude of sin(x) in ascending order.
  2. Sort by length of lists in descending order.

6. Function apply

This function is to apply a procedure to a list. Even the function takes arbitrary numbers of arguments, the first and last arguments should be a procedure and a list. The function is really convenient even it does not seem to be. 
(apply max '(1 3 2))      ⇒   3
(apply + 1 2 '(3 4 5))    ⇒  15
(apply - 100 '(5 12 17))  ⇒  66

Exercise 5

  1. Use apply to write a same function as that of Exercise 3.

7. Making Higher Order Functions

Writing higher order functions by yourself is quite easy. Functions member-if, member, and fractal are defined here as examples.

7.1. member-if and member

A function member-if takes a predicate and a list as arguments and returns a sub-list of the original whose car is the first item that satisfies the predicate. The function member-if can be defined like as follows: 
(define (member-if proc ls)
  (cond
   ((null? ls) #f)
   ((proc (car ls)) ls)
   (else (member-if proc (cdr ls)))))

(member-if positive? '(0 -1 -2 3 5 -7))
⇒  (3 5 -7)
Further, the function member that checks if the specified item is in the list can be defined like as follows. The function takes three arguments, a function to compare, the specified item, and a list: 
(define (member proc obj ls)
  (cond
   ((null? ls) #f)
   ((proc obj (car ls)) ls)
   (else (member proc obj (cdr ls)))))

(member string=? "hello" '("hi" "guys" "bye" "hello" "see you"))
⇒  ("hello" "see you")

7.2. Fractal Curves

Generating fractal curves such as C curves, Dragon curves, etc. which are generated by inserting a point(s) between two points according to a positioning function can be separated into two parts: a common routine to generate fractal curves and a positioning function. The code is like as follows: 
01:     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
02:     ;;;
03:     ;;;                frac.scm
04:     ;;;
05:     ;;;        draw fractal curves
06:     ;;;         by T.Shido
07:     ;;;       on August 20, 2005
08:     ;;;
09:     ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
10:     
11:     (define _x car)
12:     (define _y cdr)
13:     (define point cons)
14:     
15:     ;;; (rappend '(1 2 3) '(4 5 6)) -> (3 2 1 4 5 6)
16:     (define (rappend ls0 ls1)
17:       (let loop((ls0 ls0) (ls1 ls1))
18:         (if (null? ls0)
19:             ls1
20:           (loop (cdr ls0) (cons (car ls0) ls1)))))
21:       
22:     ;;; 
23:     (define (divide p1 p2 r)
24:       (point (+ (* r (_x p1)) (* (- 1.0 r) (_x p2)))
25:     	 (+ (* r (_y p1)) (* (- 1.0 r) (_y p2)))))
26:     
27:     ;;; print out data points to a file
28:     (define (print-curve points fout)
29:       (with-output-to-file fout
30:         (lambda ()
31:           (for-each
32:            (lambda (p)
33:              (display (_x p))
34:              (display " ")
35:              (display (_y p))
36:              (newline))
37:            points))))
38:              
39:     
40:     ;;; the main function to create fractal curves
41:     (define (fractal proc n points fout)
42:       (let loop((i 0) (points points))
43:         (if (= n i)
44:     	(print-curve points fout)
45:     	(loop
46:     	 (1+ i)
47:     	 (let iter ((points points) (acc '()))
48:     	   (if (null? (cdr points)) 
49:     	       (reverse! (cons (car points) acc))
50:     	       (iter
51:     		(cdr points)
52:     		(rappend (proc (first points) (second points)) acc)))))))
53:       'done)
54:     
55:     
56:     
57:     ;;; c curve
58:     (define (c-curve p1 p2) 
59:       (let ((p3 (divide p1 p2 0.5)))
60:         (list
61:          p1
62:          (point (+ (_x p3) (- (_y p3) (_y p2)))
63:     	    (+ (_y p3) (- (_x p2) (_x p3)))))))
64:     
65:     ;;; dragon curve
66:     (define dragon-curve 
67:       (let ((n 0))
68:         (lambda (p1 p2)
69:           (let ((op (if (even? n) + -))
70:     	    (p3 (divide  p1 p2 0.5)))
71:     	(set! n (1+ n))
72:     	(list
73:     	 p1
74:     	 (point (op (_x p3) (- (_y p3) (_y p2)))
75:     		(op (_y p3) (- (_x p2) (_x p3)))))))))
76:           
77:     
78:     ;;; koch curve
79:     (define (koch p1 p2)
80:       (let ((p3 (divide p1 p2 2/3))
81:     	(p4 (divide p1 p2 1/3))
82:     	(p5 (divide p1 p2 0.5))
83:     	(c  (/ (sqrt 3) 2)))
84:         (list
85:          p1
86:          p3
87:          (point (- (_x p5) (* c (- (_y p4) (_y p3))))
88:     	    (+ (_y p5) (* c (- (_x p4) (_x p3)))))
89:          p4)))
line comments
11–13 Points on the XY plane are represented by pairs whose car and cdr are x and y coordinates, respectively. Functions _x and _y are defined to get the coordinates. A function point is to make a point.
15–20 (rappend ls0 ls1)
taking two lists as arguments, and connecting the reverse of the first list to the second list.
23–25 (divide p1 p2 r)
dividing p1 and p2 internally by the ratio r.
27–37 (print-curve points fout)
Outputting a list of points (points) to fout by one point par line.
40–53 (fractal proc n points fout)
The higher order function that generate fractal curves.
proc, n, points, and fout are a positioning function, the number of repetition, a list of initial points, a file name for output data, respectively.
The function consists of a double loop named loop and iter. The loop repeats the interpolation for the data list for n times. The iter adds new points to the data list using the positioning function. In short, fractal generates curves by repeating iter for n times.
The positioning function proc takes two points as arguments and returns a list of the first point and the interpolated point.
57–63 (c-curve p1 p2)
The positioning function for C curves.
65–75 (dragon-curve p1 p2)
The positioning function for Dragon curves.
78–89 (koch p1 p2)
The positioning function for Koch curves.
Following shows how to generate fractal curves. The source code is attached here. Compile it before use to reduce calculation time. 
(compile-file "frac.scm")
(load "frac")

;; C-Curve
(fractal c-curve 14 '((0 . 0) (2 . 3)) "c14.dat")
;Value: done

;; Dragon-Curve
(fractal dragon-curve 14 '((0 . 0) (1 . 0)) "d14.dat")
;Value: done

;; Koch-Curve
(fractal koch 5 '((0 . 0) (1 . 0)) "k5.dat")
;Value: done
The x and y coordinates are stored in a file named '*.dat'. You can plot it using your favorite plotting application.

Figures 1–3 are plotted using the gnuplot.


Fig. 1: A C-Curve.


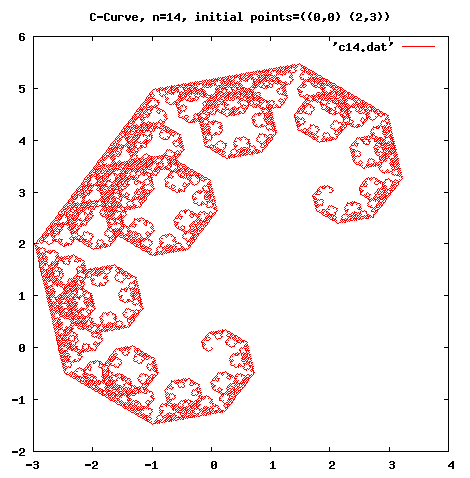
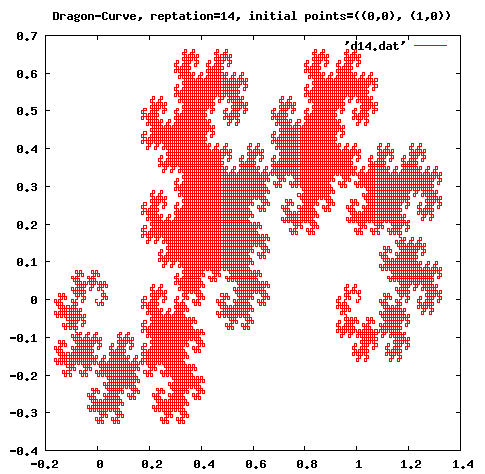
Fig. 2: A Dragon-Curve.


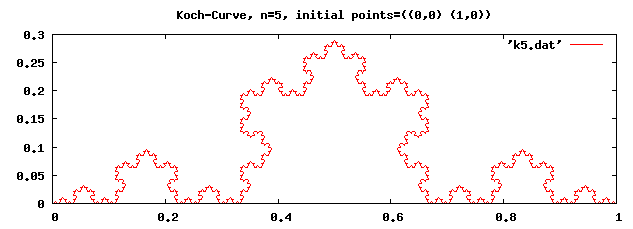
Fig. 3: A Koch-Curve.

Exercise 6

  1. Define keep-matching-items by yourself.
  2. Define map by yourself. It may be some how difficult to accept more than one list as arguments.
    The rest parameter is defined by a dot pair (.). The cdr part of the pair is sent to the function as a list.

    Example: my-list 

    (define (my-list . x) x)
    In addition, you need the function apply.

7. Summary

I have explained about higher order functions in this chapter. As shown in generating fractal curves, the higher order functions promote the modularity. You can define your own higher order functions quite easily. You should always mind it when you write functions that you can abstract more by using higher order functions, which makes your code reusable.

I will explain about IO in the next chapter.

Answers for Exercises

Answer 1


; 1
(define (double ls)
  (map (lambda (x) (* x 2)) ls))

; 2
(define (sub ls1 ls2)
  (map - ls1 ls2))

Answer 2

; 1
(define (filter-even ls)
  (keep-matching-items ls even?))
; 2
(define (filter-10-100 ls)
  (keep-matching-items ls (lambda (x) (<= 10 x 100))))

Answer 3

(define (sqrt-sum-sq ls)
  (sqrt (reduce + 0 (map (lambda (x) (* x x)) ls))))

Answer 4

; 1
(define (sort-sin ls)
  (sort ls (lambda (x y) (< (sin x) (sin y)))))

; 2
(define (sort-length ls)
  (sort ls (lambda (x y) (> (length x) (length y)))))

Answer 5

(define (sqrt-sum-sq-a ls)
  (sqrt (apply + (map (lambda (x) (* x x)) ls))))

Answer 6

; 1
(define (my-keep-matching-items ls fn)
  (cond
   ((null? ls) '())
   ((fn (car ls))
    (cons (car ls) (my-keep-matching-items (cdr ls) fn)))
   (else
    (my-keep-matching-items  (cdr ls) fn))))

; 2
(define (my-map fun . lss)
  (letrec ((iter (lambda (fun lss)
		       (if (null? lss)
			   '()
			   (cons (fun (car lss))
				 (iter fun (cdr lss))))))
	   (map-rec (lambda (fun lss)
		      (if (memq '() lss)
			  '()
			  (cons (apply fun (iter car lss))
				(map-rec fun (iter cdr lss)))))))
    (map-rec fun lss)))

(my-map + '(1 2 3) '(10 20 30) '(100 200 300))
⇒ (111 222 333)

HOME Yet Another Scheme Tutorial download Post Messages