HOME Yet Another Scheme Tutorial Post Messages

3. Making Lists

1. Introduction

As Scheme belongs to Lisp linguistic family, it is good at list operations. You should understand lists and list operations thoroughly to master Scheme. Lists play important roles in recursive functions and higher order functions, which I will explain in later chapters.

In this chapter, I will explain basic list operators, such as cons, car, cdr, list and quote.

2. Cons Cells and Lists

2.1. Cons Cells

First, let me explain about cons cells which are elements of lists. Cons cells are a memory spaces which storage two addresses. Cons cells can be made by function cons.

Give (cons 1 2) to the front end. 

(cons 1 2)
;Value 11: (1 . 2)
It responds (1 . 2). Function cons allocates a memory space for two addresses as shown in Figure 1. and stores the address to 1 in one part and to 2 in the other part. The part storing the address to 1 is called car part and that storing the address to 2 is called cdr part. Car and cdr are abbreviations of Contents of the Address part of the Register and Contents of the Decrement part of the Register. These are originated from the names of memory spaces of the hardware on which Lisp was first implemented. These names also indicate that the reality of the cons cell is a memory space. The name cons is an abbreviation of a English term 'construction' for your information.


Fig 1: A cons cell.

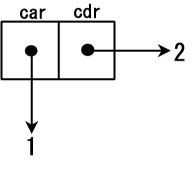
Cons cells can be beaded. 

(cons 3 (cons 1 2))
;Value 15: (3 1 . 2)
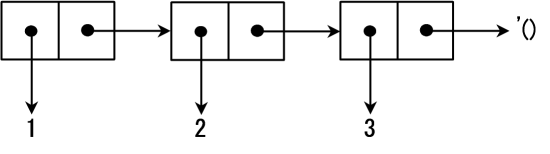
(3 1 . 2) is a convenient notation for (3 . (1 . 2)). The memory space of this situation is shown in Figure 2.


Figure 2: Beaded cons cells.

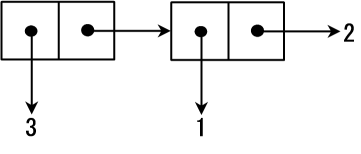
Cons cells can store different kinds of data and can be nested. 

(cons #\a (cons 3 "hello"))
;Value 17: (#\a 3 . "hello")

(cons (cons 0 1) (cons 2 3))
;Value 23: ((0 . 1) 2 . 3)
This is due to that Scheme manipulates all the data by their addresses. (#\c represents a character c. For example, #\a represents a character a.)

2.2. Lists

Lists are (beaded) cons cells with the cdr part of the last cons cell being '(). '() is called the empty list, which is included to lists. Even if the data consists of only one cons cell, it is a list if the cdr part is '(). Figure 3 shows the memory structure of a list (1 2 3).


Figure 3: Memory structure for a list (1 2 3).

Actuary, list can be defined recursively like as follows:

  1. '() is a list.
  2. If ls is a list and obj is a kind of data, (cons obj ls) is a list.
As lists are data structure defined recursively, it is reasonable to be used in recursive functions.

2.3. atoms

Data structures which do not use cons cells are called atom. Numbers, characters, strings, vectors, and '() are atom. '() is an atom and a list as well.

Exercise 1

Make data structures using cons that the front end responds like as follows.
  1. ("hi" . "everybody")
  2. (0)
  3. (1 10 . 100)
  4. (1 10 100)
  5. (#\I "saw" 3 "girls")
  6. ("Sum of" (1 2 3 4) "is" 10)

3. quote

All tokens are ready to be evaluated due to the Scheme's rule of the evaluation that tokens in parentheses are evaluated from inner to outer and that the value comes out from the outermost parentheses is the value of the S-expression. A special form named quote is used to protect tokens from evaluation. It is for giving symbols or lists to a program, which became something else by evaluation.

For instance, while (+ 2 3) is evaluated to be 5, (quote (+ 2 3)) gives a list (+ 2 3) itself to the program. As quote is frequently used, it is abbreviated as '.
For example:

Actually, '() is a quoted empty list, which means that you should write '() to represent an empty list while the interpreter responds () for an empty list.

3.1. Special forms

Scheme has two kinds of operators: One is functions. Functions evaluate all the arguments to return value. The other is special forms. Special forms are not evaluate all the arguments. Besides quote, lambda, define, if, set!, etc. are special forms.

4. Functions car and cdr

Functions that returns the car part and the cdr part of a cons cell is called car and cdr, respectively. If the value of cdr is a beaded cons cells, the interpreter prints whole values of the car parts. If the cdr part of the last cons cell is not '(), the value is also shown after .. 
(car '(1 2 3 4))
;Value: 1

(cdr '(1 2 3 4))
;Value 18: (2 3 4)

Exercise 2

Evaluated following S-expressions.
  1. (car '(0))
  2. (cdr '(0))
  3. (car '((1 2 3) (4 5 6)))
  4. (cdr '(1 2 3 . 4))
  5. (cdr (cons 3 (cons 2 (cons 1 '()))))

5. Function list

Function list is available to make a list consisting of several elements. Function list takes arbitrary numbers of arguments and returns a list of them. 
(list)
;Value: ()

(list 1)
;Value 24: (1)

(list '(1 2) '(3 4))
;Value 25: ((1 2) (3 4))

(list 0)
;Value 26: (0)

(list 1 2)
;Value 27: (1 2)

6. Summary

This chapter explained about lists and basic operations for lists. Chapters 1 – 3 may be boring, I am afraid. The next chapter is interesting, I hope. It deals with making functions. I will explain

The Answers for Exercises

Answer 1

;1
(cons "hi" "everybody")
;Value 32: ("hi" . "everybody")

;2
(cons 0 '())
;Value 33: (0)

;3
(cons 1 (cons 10 100))
;Value 34: (1 10 . 100)

;4
(cons 1 (cons 10 (cons 100 '())))
;Value 35: (1 10 100)

;5
(cons #\I (cons "saw" (cons 3 (cons "girls" '()))))
;Value 36: (#\I "saw" 3 "girls")

;6
(cons "Sum of" (cons (cons 1 (cons 2 (cons 3 (cons 4 '())))) (cons "is" (cons 10 '()))))
;Value 37: ("Sum of" (1 2 3 4) "is" 10)

Answer 2

;1
(car '(0))
;Value: 0

;2
(cdr '(0))
;Value: ()

;3
(car '((1 2 3) (4 5 6)))
;Value 28: (1 2 3)

;4
(cdr '(1 2 3 . 4))
;Value 29: (2 3 . 4)

;5
(cdr (cons 3 (cons 2 (cons 1 '()))))
;Value 31: (2 1)

HOME Yet Another Scheme Tutorial Post Messages