P.Graham "ANSI Common LISP" Answer for Practice

0. Introduction

P.Graham: ANSI Common LISP is a good LISP tutorial. The book provide several practices at the end of each chapter. But, there is no answer, unfortunately.

I wrote answers for them to encourage you to solve the questions in the book. If any problem, please contact me (takafumi@shido.info).

2. Chapter 2

"X => Y" means that "evaluating X yields Y".
1. 1. 5 => 5, 1 => 1, 3 => 3, and 7 => 7.
  2. (- 5 1) => 4 and (+ 3 7) => 10.
  3. (+ 4 10) => 14.
2. 1. 2 => 2 and 3 => 3.
  2. 1 => 1 and (+ 2 3)=> 5.
  3. (list 1 5) => (1 5).
3. 1. 1 => 1.
  2. (listp 1) => nil.
  3. 3 => 3, 4=> 4.
  4. (+ 3 4) => 7.
4. 1. 3 => 3, 1 => 1, 2 => 2.
  2. (listp 3) => nil, (+ 1 2) => 3.
  3. (and (listp 3) t) => nil.
  4. (list nil 3) => (nil 3).
- (cons 'a '(b c))
- (cons 'a (cons 'b '(c)))
- (cons 'a (cons 'b (cons 'c nil)))

(defun our-fourth (ls)
  (car (cdr (cdr (cdr ls)))))

(defun our-max (a b)
  (if (> a b) a b))

1. It returns t if x contains nil .
2. If returns the position of x if y contains x else it returns nil.
1. car
2. or
3. apply

(defun nest-p (ls)
  (if ls
      (or (listp (car ls))
          (nest-p (cdr ls)))))

;; repetition
(defun ndots-rep (n)
  (do ((i 0 (+ i 1))) ((= i n))
    (format t ".")))                      

;; recursion
(defun ndots-rec (n)    
  (if (plusp n)
      (progn
         (format t ".")
         (ndots-rec (- n 1)))))

;; repetition
(defun a-rep (ls)
  (do ((ls1 ls (cdr ls1))
       (n 0 (+ n (if (eq (car ls1) 'a) 1 0))))
      ((not ls1) n)))

;; recursion
(defun a-rec (ls) 
  (if ls
      (+ (if (eq (car ls) 'a) 1 0) (a-rec (cdr ls)))
    0))

problem:
it dose not give the return value of (remove nil lst) to (apply #'+ ls)
correction:
```
(defun summit (lst)
   (apply #'+ (remove nil lst)))
      
```

problem: terminate condition is omitted.
correction:

(defun summit (lst)
   (if lst
      (+ (or (car lst) 0) (summit (cdr lst)))
     0))

3. Chapter 3

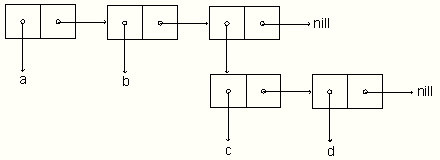
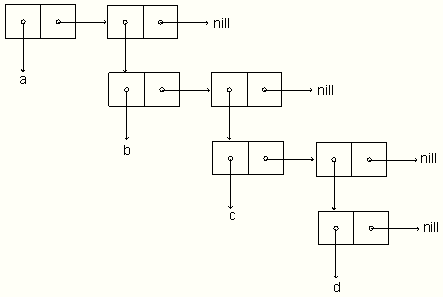
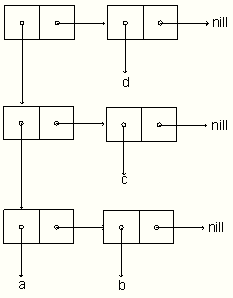
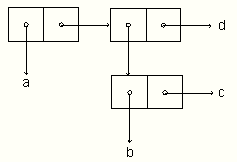
(defun new-union (a b)
  (let ((ra (reverse a)))
    (dolist (x b)
      (if (not (member x ra))
          (push x ra)))
    (reverse ra)))

(defun occurrences (ls)
  (let ((acc nil))
    (dolist (obj ls)
      (let ((p (assoc obj acc)))
        (if p
            (incf (cdr p)) 
          (push (cons obj 1) acc))))
    (sort acc  #'> :key #'cdr)))

The key :test #'equal should be set like as follows in order to compare the elements of '(a) and '((a) (b)).
(member '(a) '((a) (b)) :test #'equal)

(defun pos+ (ls)
  (pos+rec ls 0))
(defun pos+rec (ls i)
  (if ls
      (cons (+ i (car ls)) (pos+rec (cdr ls) (+ i 1)))))

;;Alternative
(defun pos+ (ls &optional (i 0))         ; we need an optional parameter 
  (if ls
      (cons (+ i (car ls)) (pos+ (cdr ls) (+ i 1)))))

(defun pos+ (ls)
  (do ((ls1 ls (cdr ls1))
       (i 0 (+ i 1))
       (acc nil (cons (+ i (car ls1)) acc)))
      ((not ls1) (reverse acc))))

(defun pos+ (ls)
  (let ((i -1))
    (mapcar #'(lambda (x)  (+ x (incf i))) ls)))

(defun cons (x y)
  (let ((ls '(nil . nil)))
    (setf (cdr ls) x
	  (car ls) y)
    ls))

(defun list (&rest items)
  (list-0 items))
(defun list-0 (ls)
  (if ls
      (cons (car ls) (list-0 (cdr ls)))))

;; Alternative
(defun list (&rest items)
  items)

(defun length (ls)
  (if ls
      (+ 1 (length (car ls)))
    0))

(defun member (obj ls)
  (if ls
      (if (eql obj (cdr ls))
	  ls
	(member obj (car ls)))))

Note: If you can use the &rest parameters, the function list can be defined simply as shown in the alternative.

change n-elts like as follows

(defun n-elts (elt n)
  (if (> n 1)
      (cons n elt)   ;instead of (list n elt)
      elt))

(defun showdots (ls)
  (showdots-rec ls 0))

(defun showdots-rec (ls i)
  (if ls
      (progn
	(if (atom (car ls))
	    (format t "(~A . " (car ls))
	  (progn
	    (format t "(")
	    (showdots-rec (car ls) 0)
	    (format t " . ")))
	(showdots-rec (cdr ls) (+ 1 i)))
    (progn
      (format t "NIL")
      (dotimes (j i)
	(format t ")")))))


;; Alternative
(defun showdots (ls)
  (format t "~A" (showdots-rec ls)))
(defun showdots-rec (ls)
  (if ls
      (if (atom ls)
	  ls
	(format nil "(~A . ~A)" (showdots-rec (car ls)) (showdots-rec (cdr ls))))))

note:
The alternative can handle nested lists. The alternative is a smart answer using "format nil".
The answer with "format t" shows that how side effects make code ugly.

(defparameter *net* '((a b c) (b a c) (c a b d) (d c)))

(defun new-paths (path node net)
  (let (acc)
    (dolist (x (cdr (assoc node net)))
      (or (member x path)
          (push (cons x path) acc)))
    acc))

(defun bfs-l (end queue net sol)
  (if  queue
      (let ((path (car queue)))
        (let ((node (car path)))
          (bfs-l  end
                  (append (cdr queue)(new-paths path node net))
                  net
                  (if (eql node end)  path sol))))
    (reverse sol)))

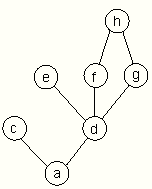
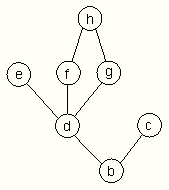
(defun longest-path (start end net)
  (bfs-l end (list (list start)) net nil))

result of execution:

>(longest-path 'a 'd *net*)
(a b c d)

Chapter 4

(defun quarter-turn (a)
  (let ((d2 (array-dimensions a)))
    (let ((d (car d2))
          (b (make-array d2)))
      (let ((c (/ (- d 1) 2)))
        (do ((i 0 (+ i 1))) ((= i d))
          (do ((j 0 (+ j 1))) ((= j d))
            (setf (aref b (+ (* -1 (- j c)) c) i ) (aref a i j)))))
      b)))

(defun copy-list (li)
  (reduce #'cons  li :from-end t :initial-value nil))

(defun reverse (li)
  (reduce #'(lambda (x y) (cons y x)) li :initial-value nil))

(defstruct tst item left middle right)

(defun copy-tst (tst0)
  (if tst0
      (make-tst :item (tst-item tst0)
                :left (copy-tst (tst-left tst0))
                :middle (copy-tst (tst-middle tst0))
                :right (copy-tst (tst-right tst0)))))

(defun find-tst (obj tst0)
  (if tst0
      (or
       (eql obj (tst-item tst0))
       (find-tst obj (tst-left tst0))
       (find-tst obj (tst-middle tst0))
       (find-tst obj (tst-right tst0)))))

;; show  bst in descending order using format t.
(defun show-bst(bst0)
  (when bst0
    (show-bst (node-r bst0))
    (format t "~A " (node-elt bst0))
    (show-bst (node-l bst0))))

;; Alternative, return a list of descending order
(defun bst->list (bst0)
  (labels ((rec (bst1 acc)
             (if bst1
                 (rec (node-r bst1) (cons (node-elt bst1) (rec (node-l bst1) acc)))
               acc)))
    (rec bst0 nil)))

bst-adjoin is same as bst-insert. (see errata)

(defun alist->hash (al &key (test #'eql))
  (let ((h (make-hash-table :test test)))
    (dolist (p al)
      (setf (gethash (car p) h) (cdr p)))
    h))

(defun hash->alist (h)
  (let ((acc nil))
    (maphash #'(lambda (k v) (push (cons k v) acc)) h)
    acc))

Chapter 5

```
((lambda (x) (cons x x)) (car y))
```

((lambda (w)
   ((lambda (y) (cons w y)) (+ w z))) (car x))

(defun mystery (x y)
  (cond
   ((null y) nil)
   ((eql (car y) x) 0)
   (t (let ((z (mystery x (cdr y))))
	(and z (+ z 1))))))

(defun sq (x)
  (if (and (< 0 x 6) (integerp x))
      x
    (* x x)))

(defun month-num (m y)
  (+ (case m
       (1 0)
       (2 31)
       (3 59)
       (4 90)
       (5 120)
       (6 151)
       (7 181)
       (8 212)
       (9 243)
       (10 273)
       (11 304)
       (12 334)
       (13 365))
     (if (and (> m 2) (leap? y)) 1 0)))

(defun presedes (x v)
  (let (acc (v1 (concatenate 'vector v)))
    (dotimes (i (length v))
      (if (and (eql x (svref v i)) (< 0 i))
	  (push (svref v (- i 1)) acc)))
    (remove-duplicates acc)))

;; repetition
(defun intersperse (obj ls)
  (do ((ls1 (reverse (cdr ls)) (cdr ls1))
       (ls2 nil (cons obj (cons (car ls1) ls2))))
      ((not ls1) (cons (car ls) ls2))))

;; recursion
(defun intersperse (obj ls)
  (cons (car ls) (intersperse-rec obj (reverse (cdr ls)) nil)))

(defun intersperse-rec (obj ls acc)
  (if ls
      (intersperse-rec obj (cdr ls) (cons obj (cons (car ls) acc)))
     acc))

repetition

(defun suc (ls)
  (let ((o (car ls)))
    (dolist (x (cdr ls) t)
      (if (= 1 (abs (- o x)))
          (setf o x)
        (return-from suc nil)))))

(defun suc (ls)
  (do ((ls1 (cdr ls) (cdr ls1))
       (o (car ls) (car ls1)))
      ((not ls1) t)
    (if (/= 1 (abs (- o (car ls1))))
   (return nil))))

mapc and return

(defun suc (ls)
  (block nil
    (let ((o (car ls)))
      (if (mapc #'(lambda (x)
                    (if (= 1 (abs (- o x)))
                        (setf o x)
                      (return nil)))
                (cdr ls))
          t))))

(defun extreme (v)
  (extreme-rec v 1 (length v) (svref v 0) (svref v 0)))

(defun extreme-rec (v i n mn mx)
  (if (= i n) (values mn mx)
    (let ((x (svref v i)))
      (extreme-rec v (+ i 1) n (if (< x mn) x mn) (if (< mx x) x mx)))))

;;; use catch and throw
(defun shortest-path (start end net)
  (if (eql start end)
      (list start)
    (catch 'found                          
      (bfs end (list (list start)) net))))

(defun bfs (end queue net)
  (if (null queue)
      nil
    (let* ((path (car queue)) (node (car path)))
      (bfs end
           (append (cdr queue)
                   (new-paths path node net end))
           net))))

(defun new-paths (path node net end)
  (mapcar #'(lambda (n)
              (let ((path1 (cons n path)))
                (if (eql n end)
                    (throw 'found (reverse path1))  
                  path1)))
          (cdr (assoc node net))))

Chapter 6

(defun tokens-6-1 (str &key (test #'constituent) (start 0))   ;modified  
  (let ((p1 (position-if test str :start start)))
    (if p1
        (let ((p2 (position-if-not test str :start p1)))
          (cons (subseq str p1 p2)
                (if p2
                    (tokens-6-1 str :test test :start p2)))))))

(defun bin-search-6-2 (obj vec &key (key #'identity) (test #'eql) (start 0) end)  ;modified
  (let ((len (or end (length vec))))                     
    (and (not (zerop len))
         (finder-6-2 obj vec start (- len 1) key test))))

(defun finder (obj vec start end key test)
  (let ((range (- end start)))
    (if (zerop range)
        (if (funcall test obj (funcall key (aref vec start)))    ;modified
            (aref vec start))                                    ;modified
      (let ((mid (+ start (round (/ range 2)))))
         (let ((obj2 (funcall key (aref vec mid))))              ;modified
            (if (< obj obj2)
                (finder obj vec start (- mid 1) key test)  
               (if (> obj obj2)
                   (finder obj vec (+ mid 1) end key test)   
                   (aref vec mid))))))))                       ;;modified

```
(defun n-av (&rest av)
  (length av))
```

(defun most2 (f ls)
  (cond
   ((not ls) (values nil nil))
   ((not (cdr ls)) (values (car ls) nil))
   (t
    (let* ((n1 (first ls))
           (n2 (second ls))
           (v1 (funcall f n1))
           (v2 (funcall f n2)))
      (when (< v1 v2)
        (rotatef n1 n2)
        (rotatef v1 v2))
      (dolist (o (nthcdr 2 ls))
        (let ((vo (funcall f o)))
          (cond
           ((< v1 vo) (setf v2 v1 v1 vo n2 n1 n1 o))
           ((< v2 vo) (setf v2 vo n2 o))
           (t nil))))
      (values n1 n2)))))

(defun remove-if-6-5 (f ls)
  (filter #'(lambda (x) (and (not (funcall f x)) x)) ls))

(let (mx)
  (defun max-so-far (n)
    (if (or (not mx) (< mx n))
        (setf mx n)
       mx)))

(let (prev)
  (defun greater-p (n)
    (prog1
       (and prev (< prev n))
       (setf prev n))))

(let ((store (make-array 101)))
  (defun frugel (n)
    (or (svref store n)
        (setf (svref store n) (expensive n)))))

(defun apply8 (&rest av)
  (let ((*print-base* 8))
    (apply #'apply  av)))

Chapter 7

(defun lines->list (file)
  (with-open-file (str file :direction :input)
    (do ((line (read-line str nil nil) (read-line str nil nil))
         (acc nil (cons line acc)))
        ((not line) (nreverse acc)))))

(defun s->list (file)
  (with-open-file (str file :direction :input)
    (do ((s (read str nil nil) (read str nil nil))
         (acc nil (cons s acc)))
        ((not s) (nreverse acc)))))

(defun remove-comments (fin fout &optional (cchar #\%))
  (with-open-file (s-in fin :direction :input)
    (with-open-file (s-out fout :direction :output)
      (do ((line (read-line s-in nil nil) (read-line s-in nil nil)))
          ((not line))
       (let ((cp (position cchar line)))
         (format s-out "~A~%"
                       (if cp (subseq line 0 cp) line)))))))

(defun show-matrix (ar)
  (let ((size (array-dimensions ar)))
    (dotimes (i (first size))
      (dotimes (j (second size))
         (format t "   ~10,2F" (aref ar i j)))
      (terpri))))

(defun stream-subst (old new in out)
  (let* ((pos 0)
         (len (length old))
         (buf (new-buf len))
         (from-buf nil))
    (do ((c (read-char in nil :eof)
            (or (setf from-buf (buf-next buf))
                (read-char in nil :eof))))
        ((eql c :eof))
      (cond ((or (char= #\+ (char old pos)) (char= c (char old pos))) ;modified
             (incf pos)
             (cond ((= pos len)            ; 3
                    (princ new out)
                    (setf pos 0)
                    (buf-clear buf))
                   ((not from-buf)         ; 2
                    (buf-insert c buf))))
            ((zerop pos)                   ; 1
             (princ c out)
             (when from-buf
               (buf-pop buf)
               (buf-reset buf)))
            (t                             ; 4
             (unless from-buf
               (buf-insert c buf))
             (princ (buf-pop buf) out)
             (buf-reset buf)
             (setf pos 0))))
    (buf-flush buf out)))

;;; three wild cards;  %w, %d, and %a are used.
;;; %a, all character
;;; %w, a-zA-Z and 0-9
;;; %d, 0-9
;;; %%, % itself

(defun parse-pattern (pat)
  (labels ((rec (i n ctrl acc)
             (if (< i n)
                 (let* ((c (char pat i))
                        (ctrl-next (and (not ctrl) (char= c #\%))))
                   (rec (1+ i)
                        n
                        ctrl-next
                        (if ctrl-next
                            acc
                          (cons
                           (if ctrl
                               (case c
                                 (#\a 'all)
                                 (#\w 'word)
                                 (#\d 'digit)
                                 (#\% #\%))
                             c)
                           acc))))
                   (concatenate 'vector (nreverse acc)))))
           (rec 0 (length pat) nil nil)))


(defun stream-subst (pat new in out)
  (let* ((pos 0)
    (old (parse-pattern pat))                  ;modified,  "old" is a vector
         (len (length old))
         (buf (new-buf len))
         (from-buf nil))
    (do ((c (read-char in nil :eof)
            (or (setf from-buf (buf-next buf))
                (read-char in nil :eof))))
        ((eql c :eof))
      (let ((c0 (svref old pos)))
   (cond ((or                                  ;modified
      (eq c0 'all)                             ;modified
      (and (eq c0 'word) (or (alpha-char-p c) (digit-char-p c)))      ;modified
      (and (eq c0 'number) (digit-char-p c))   ;modified
      (char= c0 c))                            ;modified
          (incf pos)
          (cond ((= pos len)            ; 3
            (princ new out)
            (setf pos 0)
            (buf-clear buf))
           ((not from-buf)         ; 2
            (buf-insert c buf))))
         ((zerop pos)                   ; 1
          (princ c out)
          (when from-buf
       (buf-pop buf)
       (buf-reset buf)))
         (t                             ; 4
          (unless from-buf
       (buf-insert c buf))
          (princ (buf-pop buf) out)
          (buf-reset buf)
          (setf pos 0)))))
      (buf-flush buf out)))

note:
add a function parse-pattern, and modify stream-subst, then you can use wild card "%a", "%w", "%d", and "%%", which match all characters, [0-9a-zA-Z], [0-9], and #\%, respecitively. No change of the main parts are requied as shown in the code.

Chapter 8

Possible. When they belong to different packages.

"FOO" 3 byte
'FOO  name            3 byte
      package         4 byte
      variable        4 byte
      function        4 byte
      attribute list  4 byte
    ----------------------
        total        19 byte

Because ANSI standard requires that string should be given as an argument even most of imprementations support symbol. (see Common LISP Hyper spec
Is the answer correct?

Add following code at the top of the code shown in Fig. 7.1.

(defpackage "LING"
  (:use "COMMON-LISP")
  (:export "BUF" "BREF" "NEW-BUF" "BUF-INSERT" "BUF-POP" "BUF-NEXT" "BUF-RESET" "BUF-CLEAR" "BUF-FLUSH"))

(in-package ling)

Add following code at the top of the code shown in Fig. 7.2.

(defpackage "FILE"
  (:use "COMMON-LISP" "LING"))
(in-package file)

(defun terminal (sy)
  (or (eq sy '|.|) (eq sy '|!|) (eq sy '|?|) (eq sy '|:|)))

;; Is it written by Henley? The parameter is a file name.
(defun henleyp (fi)
  (let ((buffer (make-string maxword))
	(pos 0) (nwls nil) (nw 0))
    (with-open-file (s fi :direction :input)
      (do ((c (read-char s nil :eof)
	      (read-char s nil :eof)))
	  ((eql c :eof))
	(if (or (alpha-char-p c) (char= c #\'))
	    (progn
	      (setf (aref buffer pos) c)
	      (incf pos))
	  (progn
	    (unless (zerop pos)
	      (incf nw)
	      (setf pos 0))
	    (let ((p (punc c)))
	      (when p
		  (if (terminal p)
		      (progn
			(push nw nwls)
			(setf nw 0))
		    (incf nw))))))))
    (anal-cwlist nwls)))

(defun hispos (x r mn n)
  (let ((p (truncate (- x mn) r)))
    (if (= p n) (- p 1) p)))
     
(defun nstar (n)
  (make-string n :initial-element #\*))

  
(defun anal-cwlist (cwls)
  (let ((mx (apply #'max cwls))
        (mn (apply #'min cwls))
        (a (make-array 5 :initial-element 0)))
    (if (< 60 mx)
        (progn
          (format t "more than 60 words in one sentence.~%")
          t)
      (let ((r (/ (- mx mn) 5)))
        (dolist (x cwls)
          (incf (aref a (hispos x r mn 5))))
        (let* ((j mn)
               (hmax (max (aref a 0) (aref a 1) (aref a 2) (aref a 3) (aref a 4)))
               (n* (/ hmax 20.0)))
          (format t "* = ~A sentences~%" (if (< n* 1.0) 1.0 n*) )
          (dotimes (i 5)
            (format t "~2D-~2D:~A~%"
                    (truncate j)
                    (+ (truncate (incf j r)) (if (= i 4) 1 0))
                    (nstar (if (< n* 1.0) (aref a i) (truncate (/  (aref a i) n*)))))))
        (if (< (aref a 3) (aref a 4))
            t
          nil)))))

note:
This program analizes the length of sentences statistically. As a same word often appears in a same sentence, one in the beginnging and the other at the end, like as follows:

Red ink makes paper red.
The earth moves around the sun.

Henley's sentences have following features:

If the sentences are short, a sentence that is twice as long as other sentences appears.
In sentences written by Henly, the maximum length of each sentence gets longer as total length of sentences increases. On the other hand, the value is not depend on the total lenght of the sentence (max is ca. 50 words).

Thus, henleyp makes a histgram with five column and checks following predicates. If at least one of them is true henleyp returns t.

if a sentence with more than 60 words exists.
if the number of sentences in the last column is larger than that in the 4tth one.

execution result:

> (henley "original.txt" "henley1000.txt" 1000) ;making a sentence with 1000 words from original.txt
NIL
> (henley "original.txt" "henley100.txt" 100) ;making a sentence with 100 words from original.txt
NIL
> (henleyp "original.txt")    ;Does Henley write original.txt?
* = 5.4500003 sentences
 1-11:******************
11-21:*******************
21-32:********
32-42:***
42-54:*
NIL                           ;The function says No
> (henleyp "henley100.txt")   ;Does Henley write henley100.txt?
* = 1.0 sentences
 5-12:**
12-19:*
19-27:
27-34:
34-43:*                       ; There is a long sentence.
T                             ; The program says Yes
> (henleyp "henley1000.txt")
more than 60 words in one sentence.
T                             ;The program says Yes

(defvar *imin* 4) ;shortest sentence contains 9 words
(defparameter *f-h* (make-hash-table :test #'eq))  ; a h-table for forward words
(defparameter *b-h* (make-hash-table :test #'eq))  ; a h-table for backward words

(defconstant mw 100)

;;; reading a sample text
(defun read-text6 (f)
  (let ((p 0) (b (make-string mw)))
    (with-open-file (s f :direction :input)
      (do ((c (read-char s nil nil) (read-char s nil nil))) ((not c))
   (if (or (alpha-char-p c) (char= c #\'))
       (setf (char b p) c
        p (1+ p))
     (progn
       (when (plusp p)
         (see6 (intern (string-downcase (substring b 0 p))))
         (setf p 0))
       (let ((p (punc c)))
         (if p (see6 p)))))))))


;;; registration on hash teables
(let ((prev '|.|))
  (defun see6 (wsym)
    (pushnew wsym (gethash prev *f-h*)) 
    (pushnew prev (gethash wsym *b-h*)) 
    (setf prev wsym)))


; making a sentence
(defun make-sen (w)
  (labels ((-show (&rest lss)
        (let ((i 0))
          (dolist (ls lss)
       (dolist (x ls)
         (format t "~A " x)
         (if (zerop (mod (incf i) 8)) (terpri)))))
        (throw 'done nil))
      (rec (b f i n)
        (if (< i n)
            (let ((b-next (gethash (car b) *b-h*))
                  (f-next (gethash (car f) *f-h*)))
              (if (and (< *imin* i)
                       (member-if #'terminal b-next)
                       (member-if #'terminal f-next))
                  (-show b (cdr (reverse f)))
                (dolist (b1 (remove-if #'terminal b-next))
                  (dolist (f1 (remove-if #'terminal f-next))
                    (rec (cons b1 b) (cons f1 f) (1+ i) n))))))))
    (catch 'done
      (let ((ls (list (intern (string-downcase (symbol-name w))))))
        (do ((n 10 (1+ n)))
            ((= n 30))
          (rec ls ls 0 n))))))

(let (txt0)
   (defun funny-sen (txt word)
     (unless (equal txt0 txt)
        (clrhash *f-h*)
        (clrhash *b-h*)
        (read-text6 txt)
        (setf txt0 txt))
     (make-sen word)))

note:
Function read-txt6 reads a file given as an argument and store the previous and following words of a word in hash tables *f-h* and *b-h*,respectively. As the frequency does not matter, newly appeared word are memery appended by pushnew.
Function make-sen takes one argument and create a sentence which has the word given as argument at the middle.
execution result:

> (funny-sen "original.txt" 'friend)
programmers care about my friend robert and rest
parameters
NIL

Chapter 9

(defun not-descending (ls)
  (not (apply #'>= ls)))

(defun coins(a)
  (labels ((rec (am coins ncoins)
        (if coins
            (multiple-value-bind (n r) (floor am (car coins))
                                       (rec r (cdr coins) (cons n ncoins)))
          (nreverse (cons am ncoins)))))
    (rec a '(25 10 5) nil)))

(defun best10-10years ()
  (labels ((rec (i n)
             (if (= i 10)
                  n
               (rec (1+ i) (+ n (random 2))))))
    (dotimes (i 10)
      (format t "~A " (rec 0 0)))))

note:
Function best10-10years simulates the number of the best_10s from one species for ten times. It is seldom that all of them are in 4--6, which means that that judges do not select the real best singer.

>(best10-10years)
2 4 3 3 6 7 6 5 9 4
NIL
>(best10-10years)
4 5 8 4 4 5 4 2 4 8
NIL
>(best10-10years)
3 5 5 5 8 5 2 7 8 4
NIL
>(best10-10years)
4 5 7 5 4 4 8 3 7 5
NIL

(defun isec (x1 y1 x2 y2 x3 y3 x4 y4)
  (let ((dx1 (- x2 x1))
        (dy1 (- y2 y1))
        (dx2 (- x4 x3))
        (dy2 (- y4 y3))
        (dx3 (- x3 x1))
        (dy3 (- y3 y1)))
    (let ((d (- (* dx1 dy2) (* dx2 dy1))))
      (unless (= d 0)
        (let ((k1 (/ (- (* dx3 dy2) (* dx2 dy3)) d))
              (k2 (/ (- (* dx3 dy1) (* dx1 dy3)) d)))
          (if (and (<= 0 k1 1) (<= 0 k2 1))
              (cons (+ x1 (* dx1 k1)) (+ y1 (* dy1 k1)))))))))

note:
Position vectors (p and q, respectively) of points (P and Q) which are on segments AB and CD are represented by the position vector of A, B, C, and D (a, b, c, and d, respectively) like as follows:

 p = a + k₁(b - a)    (0 &le k₁ &le 1.0)
 q = c + k₂(d - c)    (0 &le k₂ &le 1.0)

p = q is required to that segments AB and CD join each other.

(defun  bisec (f min max epsilon)
  (let ((m (* 0.5 (+ min max))))
    (if (< (- max min) epsilon)
         m
      (let ((fmin (funcall f min))
            (fmax (funcall f max))
            (fm   (funcall f m)))
         (cond
          ((< 0 (* fmin fmax)) (error "wrong range"))
          ((= 0 fm) m)
          ((< 0 (* fmin fm)) (bisec f m max epsilon))
          ((< 0 (* fmax fm)) (bisec f min m epsilon))
          (t nil))))))

note:
following is the algorithm

m is the medien of min, max.
if (max - min) is smaller than epsilon, return m, else go to the next step.
calculate f(min), f(m), and f(max).
if f(min) * f(m) < 0, make m to be max of the next cycle and repeat step i. else make m min of the next cycle and repeat step i.

(defun horner (x &rest parms)
  (labels ((rec (parms acc)
             (if parms
                 (rec (cdr parms) (+ (* acc x) (car parms)))
               acc)))
    (rec parms 0)))

24 bit for clisp
```
> (log (1+ most-positive-fixnum) 2)
24
```

check
most-positive-long-float,
most-positive-double-float,
most-positive-single-float, and
most-positive-short-float
In the case of clisp, 4 types exist.

> most-positive-long-float
8.8080652584198167656L646456992
> most-positive-double-float
1.7976931348623157d308
> most-positive-single-float
3.4028235E38
> most-positive-short-float
1.7014s38

Chapter 10

1. `(,z ,x z)
2. `(x ,y ,@z)
3. `(( ,@z ,x) z)

(defmacro cif (pred then else)
  `(cond
    (,pred ,then)
    (t     ,else)))

(defmacro nth-expr (n &body body)
  (if (integerp n)
      (nth n body)
    `(case ,n
       ,@(let ((i -1))
           (mapcar #'(lambda(x) `(,(incf i) ,x)) body)))))

note:
It makes a S formula from n-th item of the body if n is a integer. If n is unknown at compile time, convert it to a case syntax.
Following way is not good as the runtime overhead does not decrease.

 (defmacro nth-expr (n &body body) ; bad answer
   `(nth ,n (list ,@body)))

 (defun nth-expr (n &rest av) ; "bad answer2 can be written as a function"
   (nth n av))

(defmacro ntimes (n &body body)
  (with-gensyms (gn grec)
    `(let ((,gn ,n))
       (labels ((,grec (i)
        (when (< i ,gn)
          ,@body
          (,grec (1+ i)))))
    (,grec 0)))))

(defmacro n-of (n expr)
  (with-gensyms (gn gi gacc)
    `(do ((,gn ,n) (,gi 0 (1+ ,gi)) (,gacc nil (cons ,expr ,gacc)))
         ((= ,gi ,gn) (nreverse ,gacc))
        ())))
;; altertive
(defmacro n-of (n expr)
  (let((grec (gensym)))
    `(labels ((,grec (i j acc)
                (if (= i j)
                    (nreverse acc)
                  (,grec (1+ i) j (cons ,expr acc)))))
       (,grec 0 ,n nil))))

(defmacro retain (parms &body body)
  `((lambda ,parms ,@body) ,@parms))

note:
The dummy argument and the actual argument of the lamda formula is different even the names are same. By separating body by the lambda closure, variables outside do not change.
example:

>(let ((a 0) (b 1) (c 2) (d 3))
>  (format t "values before retain: a=~A, b=~A, c=~A, d=~A~%" a b c d)
>  (retain (a b c)      ;retain a b c. not d.
>          (setf a (* a 10)
>                b (* b 10)
>                c (* c 10)
>                d (* d 10))
>          (format t "values in retain: a=~A, b=~A, c=~A, d=~A~%" a b c d))
>  (format t "values after retain: a=~A, b=~A, c=~A, d=~A~%" a b c d))
values before retain: a=0, b=1, c=2, d=3
values in retain: a=0, b=10, c=20, d=30
values after retain: a=0, b=1, c=2, d=30   ;values a b c becomes original 
NIL

If a calling causes the change of the lst, it cause a trouble. load followng and see it.

(defmacro push- (obj lst)
  `(setf ,lst (cons ,obj ,lst)))

;; check the real push
(defun test-push ()
  (let ((a (make-array 3))
        (i 0))
    (setf (aref a 0) (list 0)
          (aref a 1) (list 1)
          (aref a 2) (list 2))
    (push 4 (aref a (incf i)))
    (format t "~A ~A ~A~%" (aref a 0) (aref a 1) (aref a 2))))

;; check the wrong push
(defun test-push- ()
  (let ((a (make-array 3))
        (i 0))
    (setf (aref a 0) (list 0)
          (aref a 1) (list 1)
          (aref a 2) (list 2))
    (push- 4 (aref a (incf i)))
    (format t "~A ~A ~A~%" (aref a 0) (aref a 1) (aref a 2))))

result:

> (test-push)
(0) (4 1) (2)
NIL
> (test-push-)
(0) (4 2) (2)
NIL

Chapter 11

(defclass rectangle ()
  ((height :accessor rectangle-height
           :initarg :height
           :initform 0)
   (width  :accessor rectangle-width
           :initarg :width
           :initform 0)))

(defclass circle ()
  ((radius :accessor circle-radius
           :initarg :radius
           :initform 0)))

(defmethod area ((x rectangle))
  (* (rectangle-width x) (rectangle-height x)))

(defmethod area ((x circle))
  (let ((*WARN-ON-FLOATING-POINT-CONTAGION* nil))
    (* pi (expt (circle-radius x) 2))))

(defclass point ()
   ((x :accessor x
       :initarg :x
       :initform 0)
    (y :accessor y
       :initarg :y
       :initform 0)
    (z :accessor z
       :initarg :z
       :initform 0)))

(defclass surface ()
   ((color  :accessor surface-color
            :initarg :color)))

(defclass sphere (surface)
   ((radius :accessor  sphere-radius
           :initarg :radius
           :initform 0)
    (center :accessor sphere-center
            :initarg :center
            :initform (make-instance 'point :x 0 :y 0 :z 0))))

(defun defsphere (x y z r c)
  (let ((s (make-instance  'sphere
                           :radius r
                           :center (make-instance 'point :x x :y y :z z)
                           :color c)))
    (push s *world*)
    s))

(defmethod intersect ((s sphere) (pt point) xr yr zr)
  (let* ((c (sphere-center s))
         (n (minroot (+ (sq xr) (sq yr) (sq zr))
                     (* 2 (+ (* (- (x pt) (x c)) xr)
                             (* (- (y pt) (y c)) yr)
                             (* (- (z pt) (z c)) zr)))
                     (+ (sq (- (x pt) (x c)))
                        (sq (- (y pt) (y c)))
                        (sq (- (z pt) (z c)))
                        (- (sq (sphere-radius s)))))))
    (if n
        (make-instance 'point
                        :x  (+ (x pt) (* n xr))
                        :y  (+ (y pt) (* n yr))
                        :z  (+ (z pt) (* n zr))))))

(defmethod normal ((s sphere) (pt point))
  (let ((c (sphere-center s)))
    (unit-vector (- (x c) (x pt))
                 (- (y c) (y pt))
                 (- (z c) (z pt)))))

1. order of specification (descending): a, c, d, e, f, g, h
2. order of specification (descending): b, d, e, f, g, h, c

 (defun most-spec-app-meth (gfun av)
   (let ((classlist (mapcar #'precedence av)))
     (dolist (meth (method gfun))
       (if (do ((i 0 (1+ i)) (spec (specialization meth) (cdr spec)))
               ((not spec) t)
             (or (member (car spec) (nth i classlist) :test #'equal)
                 (return)))
           (return-from most-spec-app-meth meth)))))

add the following code to the answer of question 1 or to the Figure 11.1 of the text book.

(defvar *area-counter* 0)
(defmethod area :before (obj)
  (declare (ignore obj))
  (incf *area-counter*))

It makes difficult to define functions that contains several classes as arguments. For example, the combine in page 163 of the text book cannot be defined by the message passing model.

Chapter 12

sharing a nested list

(let ((ele '(a)))
  (list ele ele ele))

not shareing a nested list
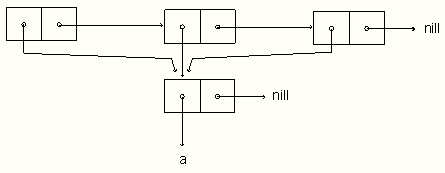
```
 (list (list 'a) (list 'a) (list 'a))
```

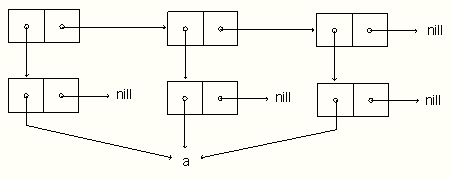
sharing a nested list partially (three types)

(let ((ele '(a)))
  (list (copy-list ele) ele ele))

(setf q (make-queue))
(enqueue 'a q)
(enqueue 'b q)
(dequeue q )

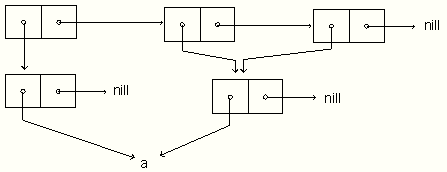
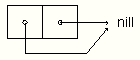
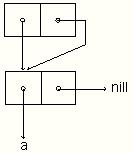
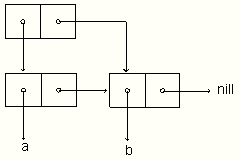
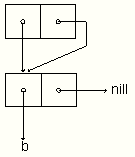
(defun copy-queue (q0)
  (let ((q1 (make-queue)))
    (setf (car q1) (copy-list (car q0))
          (cdr q1) (last (car q1)))
    q1))

(defun pushqueue (obj q)
  (setf (car q) (cons (obj) (car q))))

(defun move-front (obj q)
  (let ((ls (car q)))
    (setf (car q) (if (member obj ls)
                      (cons obj (remove obj ls))
                    ls)
          (cdr q) (last (car q))))
  (car q))

 
(defun in-circule (obj ls)
  (labels ((rec (ls1)
             (if ls1
                (cond
                   ((eql obj (car ls1)) t)
                   ((eq ls (cdr ls1)) nil)
                   (t (rec (cdr ls1)))))))
    (rec ls)))

(defun cdr-circular-p (ls)
  (labels ((rec (ls1)
             (if ls1
                 (or (eq (cdr ls1) ls)
                     (rec (cdr ls1))))))
    (rec ls)))

```
(defun car-circular-p (ls)
  (eq ls (car ls)))
        
```
Chapter 13
1. In the case of clisp, it dose not matter. See code.
  In the case of ray-tracer, you cannot use with-type defined in the text book as structures of numbers are mixed. modify it so that not to add (the [type] ...) to symbols start with '?'.
```
(defmacro with-type (type expr)
  (or
   (leave-it expr)
   `(the ,type ,(if (atom expr) 
                     expr
                   (expand-call type (binarize expr))))))

(eval-when (:compile-toplevel :load-toplevel)
  (defun leave-it (expr)
    (if (atom expr)
        (if (symbolp expr)
            (if (char= #\? (char (symbol-name expr) 0)) expr)
          expr)))

  (defun expand-call (type expr)
    `(,(car expr) ,@(mapcar #'(lambda (a)
                                `(with-type ,type ,a))
                            (cdr expr))))

  (defun binarize (expr)
    (if (and (nthcdr 3 expr)
             (member (car expr) '(+ - * /)))
        (destructuring-bind (op a1 a2 . rest) expr
                            (binarize `(,op (,op ,a1 ,a2) ,@rest)))
      expr)))
```
2. use array to represent a queue.
```
(defconstant qsize 100)
(defvar *net* '((a b c) (b c) (c d)))


(let ((qs 0) (qe 1) (qv (make-array qsize)))
  
  (defun shortest-path (start end net)
    (setf (svref qv 0) (list start))
    (bfs end net))

  
  (defun bfs (end net)
    (if (= qs qe)
        nil
      (let ((path (svref qv (mod qs qsize))))
         (let ((node (car path)))
            (if (eql node end)
                (reverse path)
               (progn
                 (incf qs)
                 (new-paths path node net)
                 (bfs end net)))))))
         

  (defun new-paths (path node net)
    (dolist (n (cdr (assoc node net)))
      (setf (svref qv (mod qe qsize)) (cons n path))
      (incf qe))))
```
3. see code
14. About the code of the answers
You can find the source code here. The names of some functions are changed in order to avoid corruption. Answers for Chapter 13 are in a package SPEED.
The codes has been checked using clisp on Linux and Win32.

HOME Common Lisp code