行列計算ライブラリー
1. はじめに
行列計算も LISP が得意な分野の一つです。
LISP は少なくとも7次元までの配列を扱うことが出来、各次元には少なくとも 1023 の
要素が持てます。
しかし、LISP で行列に値を代入するのは面倒くさく注1,2、短いコードがかけるという
LISP の利点が損なわれてしまっています。そこで、行列計算用ライブラリーを作成しました。
このライブラリーの目的は、マクロを使うことによって行列への代入を簡単にすることと、
頻繁に使用する関数を作成することです。
注1:例えば、元の行列の要素 (m[i][j])
にある値 vをかけて、それを元の行列に代入する
という操作は、C では表1の左の様に簡単に記述できます。一方 LISP では表1の右の様に長ったらしくなります。
注2:setf は参照関数と代入関数を1つにまとめ、言語仕様をコンパクトにしましたが、その一方で、
タイピング量が増加するという副作用があります。
| 表1:行列の要素への代入の方法 |
| C 言語による表記 | LISP による表記 |
|---|
| 値の代入 | m[i][j]=v; | (setf (aref m i j) v) |
|---|
| 値の操作 | m[i][j]*=v; | (setf (aref m i j) (* v (aref m i j)) |
|---|
|
2. 準備
2.1. コンパイル、ロード
コンパイル、ロードは以下の手順で行います。
- ダウンロードした matrix.lzh を適当なディレクトリで解凍します。
matrix.lisp, sample.dat の2つのファイルが生成します。
- DOS 窓を開いてそのディレクトリに行き、CLISP を立ち上げます。
- matrix.lisp をコンパイルしてロードします。
(compile-file "matrix.lisp")
(load "matrix")
2.2. LISP で行列を入力する方法
LISP でベクトル、行列を定義するには、直接定義するか、make-array を使って定義する2つの
方法があります。make-array を使うほうがタイプ量は多いのですが、詳細な定義が出来ます。
:element-type は明記しておくと計算が速くなります。
ベクトル、行列の定義方法は以下の通りです。詳しいことは
Lisp.org や
Franz.com
を見てください。
- ベクトルの定義
- (setq v0 #( n1 n2 .... ni))
(setq v0 (make-array n :intial-element 0.0d0 :element-typle 'double-float))
- 行列の定義
- (setq m0 #2A(( n1,1 n1,2) ....(.. ni,j...)))
(setq m0 (make-array '(n1 n2) :intial-element 0.0d0 :element-typle 'double-float))
3. ライブラリに収録されているマクロ、関数
- v-ip (macro)
- usage:
- (v-ip v1 v2)
- (v-ip (ma i _) (mb _ j))
- (v-ip (m i _) v)
ベクトル v1 v2 の内積を計算します。
行列の計算にも利用できます。
ベクトルの内積の計算は単純にベクトルを並べて書けばよく、
一方、行列の要素を用いた計算では、 usage 2, 3 にあるように、積の和を計算したい変数を
"_" であらわします。
usage 2 では、式1が、usage 3 では式2が計算されます。
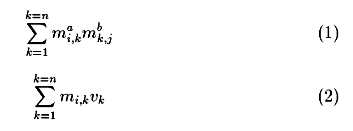
- aset (macro)
- usage:
(aset (m1 i1 j1) val1
(m2 i2 j2) val2 .....
(mk ik jk) valk ....
(mn kn jn) valn)
行列やベクトルに値をセットします。setf の様に複数の値をまとめてセットできます。
-
- a+=, a-=, a*=, a/= (macro)
- usage:
(a?= (m i j) val),
(a?= (v i) val)
C 言語の +=, -=, *=, /= と同様の働きをします。
表2にこのマクロの記法、標準の LISP の記法、 C 言語の記法を示します。
表2:a?=, LISP 標準, C 言語の記法の比較
| マクロ a?= の記法 |
標準 LISP 記法 |
C 言語の記法 |
| (a+= (m i j) val) |
(setf (aref m i j) (+ (aref m i j) val)) |
m[i][j]+=val |
| (a-= (m i j) val) |
(setf (aref m i j) (- (aref m i j) val)) |
m[i][j]-=val |
| (a*= (m i j) val) |
(setf (aref m i j) (* (aref m i j) val)) |
m[i][j]*=val |
| (a/= (m i j) val) |
(setf (aref m i j) (/ (aref m i j) val)) |
m[i][j]/=val |
- m+, m- (function)
- usage: (m+ m obj)
行列の足し算、引き算を行います。obj が行列のとき式3の様に要素ごとに足した(引いた)行列を
返します。obj がスカラーの場合、全ての要素にその数を足した(引いた)行列を返します。(式4)
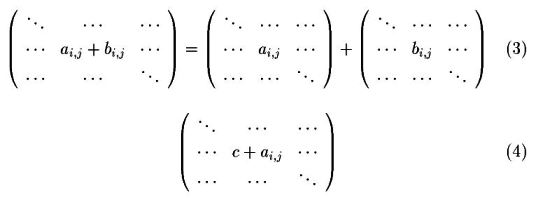
- m* (function)
- usage: (m* m obj)
行列と、スカラー、ベクトル、行列の掛け算をします。
- obj がスカラーのとき各要素にその数をかけた行列を返します。(式5)
- obj がベクトルのときベクトルに m を作用させて生じるベクトルを返します。(式6)
- obj が行列のとき、行列の積を返します、(式7)
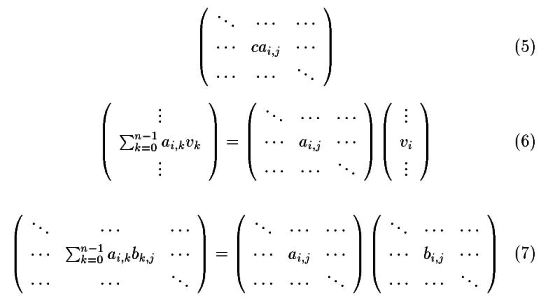
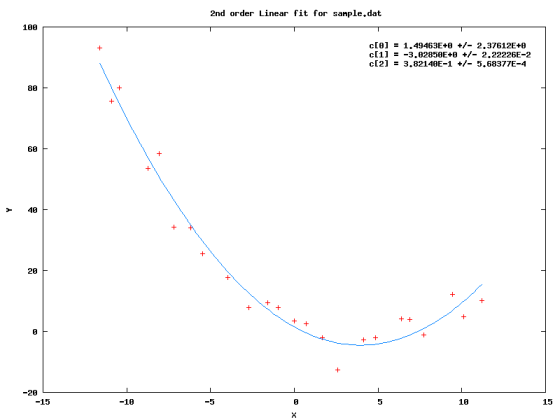
図1:(lfit 2 "sample.dat") の結果
- umat (function)
-
usage: (umat n)
n 次の単位行列を返します。
- det (function)
-
usage: (det m)
m が正方行列の時、行列式を返します。
- m-1 (function)
-
usage: (m-1 m)
m が正方行列の時、逆行列を返します。
- m-t (function)
-
usage: (m-t m)
転置行列を返します。
- m-eql (function)
-
usage: (m-eql m1 m2)
二つの行列 m1, m2 が等しいとき真を、等しくないとき偽を返します。
- lfit (function)
-
usage: (flit n data-file-name)
data-file-name の名前のファイルに保存されているデータに対して n 次の線形最小二乗法を
適用し、結果を gnuplot で示します。図1に sample.dat を 2 次でフィットした結果を示します。
データファイルのフォーマットは、sample.dat に示すように、
1行に x y の組が並んだものである必要があります。また、行頭に '#' のある行はスキップします。
- jacob (function)
-
usage: (jacob m)
ヤコブ法を用いて対称行列の固有値と固有ベクトルを求めます。
アルゴリズムは 科学技術計算ハンドブックから
借用しました。
- eigen (function)
-
usage: (eigen m)
Householder 法と QR 分解法を組み合わせて正方行列の固有値を求めます。
これもアルゴリズムは 科学技術計算ハンドブックから
借用しました。
4. 補足
4.1 マクロ a=op
マクロ a+=, a-=, a*=, a/= はマクロ生成マクロ a=op によって生成しています。a=op は
四則演算に限らずユーザー定義関数を含めた全ての関数を引数に取ることが出来ます。
例えば、
(a=op expt log sin cos)
とすると、
aexpt=, alog=, asin=, acos= というマクロが生成され、それらは表3の様な書式を取ります。
(asin=, acos= は名前が少し紛らわしいのですが。)
表3: a=op で生成されるマクロの書式と標準の書式の比較
| マクロ a=op を使った書式 |
標準での書式 |
| (aexpt= (a i j) val) |
(setf (aref a i j) (expt (aref a i j) val)) |
| (alog= (a i j) val) |
(setf (aref a i j) (log (aref a i j) val)) |
| (asin= (a i j)) |
(setf (aref a i j) (sin (aref a i j))) |
| (acos= (a i j)) |
(setf (aref a i j) (cos (aref a i j))) |
4.2 組み込みマクロ without-floating-point-underflow
ヤコブ法、ハウスホルダー法、QR分解法では、非対角成分を小さくする操作をします。
行列の要素はこのライブラリーでは double-float に規定してあるので、絶対値が 2.225d-308 より小さくなると
floating-point-underflow というエラーを起こします。
エラーを起こすルーチンを (without-floating-point-underflow ..........) で囲うことにより
このエラーを回避することが出来ます。
5. バグ
- m-1: 要素が浮動小数点の行列では、誤差が大きくなる。
6. おわりに
数値計算で LISP が使われていない最大の理由の1つは(LISP があまりメジャーではないという理由を除き)
行列の計算をするプログラムを書くとき、タイプ量が
C や Fortran で書くより増えてしまうことではないでしょうか。しかし適切なマクロ
(例えば v-ip, aset, a=op)を使うことによりタイプ量を減らすことが出来ます。さらに、関数
m+, m-, m* を定義することによって、C や Fortran
では必ず書かなければならなかった要素の積の和を求めるループを書かずに済ますことが出来ます。
特に m* は LISP の特徴である実行時型指定によっていろいろなタイプのデータを2番目の引数
に取ることができます。
LISP は強力な macro を備えているので、自分のプログラミングにあわせて自由に構文を定義する
ことが出来ます。LISP のマクロの書き方については
On Lisp を見てください。
現在進行中ながら日本語版 もあります。
両方ともフリーでダウンロードできます。
私自身も機会をみてマクロの書き方を解説してみようと思います。一般の LISP の教科書はマクロをおざなり
にしていますが、実はとても便利な機能です。適切な説明を受け、少し練習すれば簡単に書けるようになります。
 HOME
HOME Common Lisp
Common Lisp download
download 書き込む
書き込む HOME
HOME Common Lisp
Common Lisp download
download 書き込む
書き込む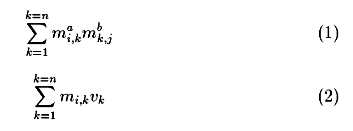
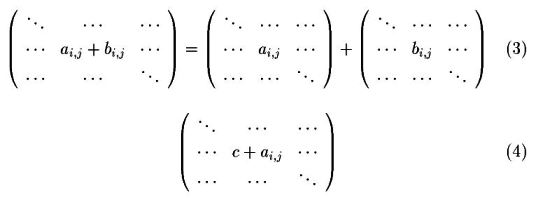
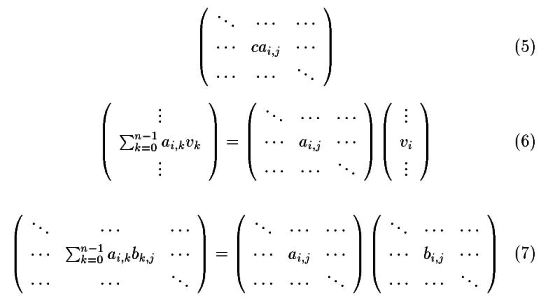

 HOME
HOME Common Lisp
Common Lisp download
download 書き込む
書き込む